A Simple Propagator

The description of the implementation of real-interval constraints is closed with the discussion of the propagation function of a simple propagator, namely a propagator for the constraint 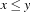$x \le y$ . The rest of the class definition of that propagator is similar to other propagators and therefore omitted here.

OZ_Return RILessEq::propagate(void)
{
  RIVar x(_x), y(_y);
   
  // step (1)
  if (x->upperBound() <= y->lowerBound()) {
    x.leave(); y.leave();
    return OZ_ENTAILED;
  }
 
  // step (2)
  if((*x <= y->upperBound()) < 0.0)  
    goto failure;
 
  // step (3)
  if((*y >= x->lowerBound()) < 0.0)  
    goto failure;
 
  return (x.leave() | y.leave())  
    ? OZ_SLEEP : OZ_ENTAILED;
 
failure:
  x.fail(); y.fail();
  return OZ_FAILED;
}

Assume that the propagator stores in its state references to its parameters on the Oz heap by the members OZ_Term _x, _y;. The function propagate() obtains access to the constraint store by declaring two instances of class RIVar and passing the Oz terms _x and _y as arguments.

The propagation proceeds in three steps.

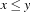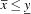Test if the constraint $x \le y$ is subsumed by the constraint store, i. e., $\overline{x} \le \underline{y}$ .
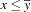Constrain the upper bound of : $x \le \overline{y}$ .
That is implemented by ri_float RI::operator <= (ri_float).
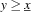Constrain the lower bound of : $y \ge \underline{x}$ .
That is implemented by ri_float RI::operator >= (ri_float).

As said in Section ``The Actual Real-Interval Constraint'' these operators return the width of the computed constraint. A width less than 0 indicates that the constraint has become inconsistent and propagation branches to label failure.

The function OZ_CtVar::leave() returns OZ_True if the constraint does not denotes a value. This is used to detect whether the propagator has to be rerun (indicated by OZ_SLEEP) or not (indicated by OZ_ENTAILED).

The return value OZ_FAILED informs the runtime system that the constraint is inconsistent with the constraint store.