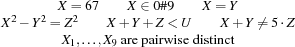2.1 Finite Domains and Constraints
A finite domain is a finite set of nonnegative integers. The notation 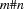 stands for the finite domain
stands for the finite domain 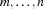 .
.
A constraint is a formula of predicate logic. Here are typical examples of constraints occurring with finite domain problems:
domain constraints
A domain constraint takes the form 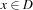 , where
, where 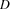 is a finite domain. Domain constraints can express constraints of the form
is a finite domain. Domain constraints can express constraints of the form 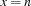 since
since 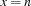 is equivalent to
is equivalent to 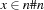 .
.
basic constraints
A basic constraint takes one of the following forms: 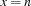 ,
, 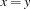 , or
, or 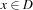 , where
, where 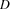 is a finite domain.
is a finite domain.
finite domain problems
A finite domain problem is a finite set 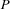 of quantifier-free constraints such that
of quantifier-free constraints such that 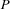 contains a domain constraint for every variable occurring in a constraint of
contains a domain constraint for every variable occurring in a constraint of 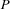 . A variable assignment is a function mapping variables to integers.
. A variable assignment is a function mapping variables to integers.
solutions
A solution of a finite domain problem 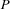 is a variable assignment that satisfies every constraint in
is a variable assignment that satisfies every constraint in 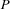 .
.
Notice that a finite domain problem has at most finitely many solutions, provided we consider only variables that occur in the problem (since the problem contains a finite domain constraint for every variable occurring in it).