4.2 General Purpose Search Engines

This section describes the search engines found in the module Search. All of these engines support recomputation, the possibility to stop their execution and various kinds of output.

Recomputation.

Scripts which create a large number of variables or propagators or scripts for which the search tree is very deep might use too much memory to be feasible. The search engines described in this section feature support for so-called recomputation. Recomputation reduces the space requirements for these scripts in that it trades space for time.

Search engines that do not use recomputation, create a copy of a computation space in each distribution step. This copy is needed such that the engine is able to follow more than one alternative of a choice.

If, for instance, a single solution search engine finds a solution after 200 distribution steps (i. e. the search tree has a depth of 201), 200 copies are created and stored by the engine.

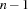Recomputation reduces the number of copies needed: Instead of creating a copy in each distribution step, only every -th distribution step a copy is created. A space for which no copy has been created can be recomputed from a copy located higher above in the search tree by recomputing some distribution steps. In the worst case, distribution steps have to be recomputed. The parameter is the so-called recomputation distance. A recomputation distance of means that the space needed decreases by a factor of and that the time needed increases by a factor of .

The following search engines take the recomputation distance as an argument (it is denoted by RcdI). A value of 2 for RcdI means that only each second distribution step a copy is created. The value 1 for RcdI means that in each distrbution step a copy is created, that is no recomputation is used. Values less than 1 mean that none but an initial copy is created: from this initial copy all other spaces are recomputed.

Recomputation can also reduce both space and time requirements. Searching a single solution of a script which features a good heuristic (i. e. there are only very few failures) creates copies which are not used. Recomputation avoids this, resulting in improvement with respect to both space and time.

Killing the Engine.

All engines described in this section return a nullary procedure, which is denoted by +KillP. Applying this procedure kills the search engine.

A search engine, which can be stopped and resumed is described in Section Section 4.3.

Different Types of Output.

Each of the engines is provided with three different types of output. The first kind returns a list of solutions as the engines in Section 4.1. The second kind returns a list of unary procedures. Applying one of these procedures merges a copy of the succeeded space and gives reference to its root variable variable by the actual argument of the procedure application. The third kind returns a list of succeeded spaces.

4.2.1 Single Solution Search

one.depth

{Search.one.depth +ScriptP +RcdI  
                  ?KillP ?Xs}

returns a singleton list containing the first solution of the script +ScriptP (a unary procedure) obtained by depth-first search. If no solution exists, nil is returned.

For instance, the procedure Search.base.one (see Section 4.1) can be defined as:

fun {Search.base.one ScriptP}
   {Search.one.depth ScriptP 1 _}
end

Suppose that Script is a script for which search does not terminate because it keeps on creating choices forever. It could look like the following:

proc {Script X}
   ··· 
   choice {Script X} [] {Script X} end 
end

If Search.one.depth is applied to this particular script by

Solutions={Search.one.depth Script 1 KillP}

the search engine can be killed by applying KillP as follows:

{KillP}

Note that a script which keeps on computing forever even without search (i. e., because it contains an infinite recursion or loop) can not be killed.

one.depthS

{Search.one.depthS +ScriptP +RcdI  
                   ?KillP ?Spaces}

returns a singleton list containing the first succeeded space for the script +ScriptP (a unary procedure) obtained by depth-first search. If no solution exists, nil is returned.

one.depthP

{Search.one.depthP +ScriptP +RcdI  
                   ?KillP ?Ps}

Similar to Search.one.depthS, but returns a list of unary procedures as output.

Search.one.depthP can be defined using Search.one.depthS as follows:

fun {Search.one.depthP Script RcdI ?KillP}
   {Map thread 
           {Search.one.depthS Script RcdI ?KillP}
        end 
        fun {$ SuccSpace}
           proc {$ Root}
              {Space.merge SuccSpace Root}
           end 
        end}
end

one.bound

{Search.one.bound +ScriptP +BoundI +RcdI ?KillP ?Xs}

one.boundS

{Search.one.boundS +ScriptP +BoundI +RcdI ?KillP ?Spaces

one.boundP

{Search.one.boundP +ScriptP +BoundI +RcdI ?KillP ?Ps

returns a singleton list containing the first solution of the script +ScriptP (a unary procedure) obtained by depth-first search, where the depth of the search tree explored is less than or equal to +BoundI.

If there is no solution in a depth less than or equal to +BoundI, but there might be solutions deeper in the tree, cut is returned. In case the entire search tree has a depth less than +BoundI and no solution exists, nil is returned.

Otherwise the output is a singleton list containing the solution (Search.one.bound), a succeeded space (Search.one.boundS), or a procedure (Search.one.boundP).

For instance

{Search.one.bound proc {$ X}
                     choice fail [] fail end 
                  end 
                  1 1 _}

returns the output nil, whereas

{Search.one.bound proc {$ X}
                     choice  
                        choice fail [] fail end 
                     [] choice fail [] fail end 
                     end 
                  end 
                  1 1 _}

returns the output cut.

one.iter

{Search.one.iter +ScriptP +RcdI ?KillP ?Xs}

one.iterS

{Search.one.iterS +ScriptP +RcdI ?KillP ?Spaces}

one.iterP

{Search.one.iterP +ScriptP +RcdI ?KillP ?Ps}

returns a singleton list containing the first solution of the script +ScriptP (a unary procedure) obtained by iterative deepening depth-first search. If no solution exists, nil is returned.

Iterative deepening applies Search.one.bound to +ScriptP with depth-bounds 1, 2, 4, 8, ... until either a solution is found or Search.one.bound returns nil.

4.2.2 All Solution Search

all

{Search.all +ScriptP +RcdI ?KillP ?Xs}

allS

{Search.allS +ScriptP +RcdI ?KillP ?Spaces}

allP

{Search.allP +ScriptP +RcdI ?KillP ?Ps}

returns the list of all solutions of the script +ScriptP (a unary procedure) obtained by depth-first search.

The output is a list of solutions (Search.all), a list of succeeded spaces (Search.allS), or a list of procedures (Search.allP).