12 Logic Programming

Many problems, especially frequent in the field of Artificial Intelligence, and also found elsewhere, e.g., in operations research, are currently solvable only by resorting to some form of search and constraint propagation. Such problems can be specified very concisely, if the programming language abstracts away the details of search by providing don't know nondeterminism. Logic programming and Prolog is considered a suitable formalism for this class of problems. In this chapter we will talk about how to express logic programming and concurrent constraint programming in Oz. In logic programming each procedure can be interpreted as a relation expressed by a logical statement. We will also discuss the relation between Oz and Prolog, and how most Prolog programs have a straight forward translation to Oz programs. For more advanced constraint solving techniques, the reader may look to the companion tutorial on constraint programming in Oz.

Warning:Please note that the material in this chapter is still incomplete.

12.1 Constraint Stores

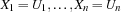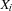Oz threads share a store where variable bindings are stored in the form of equalities: where are variables and 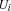are either Oz entities or variables. The constraint store contains the Oz values corresponding to records, numbers, names or variables, and the names that uniquely idententifies the procedures, cells and the various types of chunks (classes, objects, functors, etc.). Conceptually the store is modeled as a conjunctive logical formula: 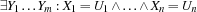, where the 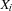are the variables and 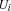are Oz values or variables, and 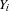are the union of all variables occuring in 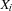and 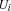. The store is said to be a constraint store. An Oz computation store consists of a constraint store, a procedure store where procedures reside, and a cell store where cells and object states reside.

12.2 Computation Spaces

A computation space consists in general of a computation store and a set of executing threads. What we have seen so far is a single computation space. When dealing with logic programming a more elaborate structure will arise with multiple nested computation spaces. The general rules for the structure of computation spaces are as follows.

• There is always a topmost computation space where threads may interact with the external world. A thread trying to add inconsistent constraints (bindings) to the store of the top space will raise a failure exception in the thread. The addition of the inconsistent constraints will be aborted and the constraint store remains always consistent.

• A thread may create a local computation space either directly or indirectly as will be shown in this section. The new computation space will be a child space and the current one the parent space. In general a hierarchy of computation spaces may be created.

• A thread belongs always to one computation space. Also, variables belong to only one computation space.

• A thread in a child space sees and may access variables belonging to its space as well as to all ancestor spaces. The converse is false. A thread in a parent space cannot see the variables of a child space, unless the child space is merged with the parent. In such a case, the child space disappears, and all its content is added to the parent space. The space merge operation may occur due to an explicit operation, or indirectly due to a language construct as will be seen in this section.

• A Thread in a child space my add constraints (bindings) on variables visible to it. This means that it may bind variables belonging to its space or to its ancestor spaces. The binding will only be visible in the current space and all its children spaces if any.

12.3 Constraint Entailment and Disentailment

A condition is entailed by the store if , considered as a logical formula, is logically implied by the store , again considered as a logical formula. Intuitively entailment of means that adding to the store does not increase the information already there. Everything is already there.

A condition is disentailed by the store if the negation of is logically implied by the store . A disentailed constraint is inconsistent with the information already in the store.

Since a constraint store is a logical formula, we can also talk of a constraint store being entailed, or disentailed by another constraint store. A space 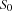is entailed (disentailed) by another space 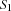if the constraint store of 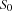is entailed (disentailed) by the constraint store if .

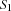We call a space that is disentailed (normally by a parent space) a failed space .

12.3.1 Examples

Consider the store 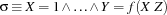and the following conditions:

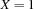• is entailed since adding this binding does not increase the information in the store.

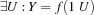• is also entailed. Adding this information does not increase our information. There is a 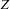that satisfies the above condition. Notice that we do not know which value 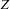will assume. But whatever value assumed by 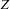, the condition would be still satisfied.

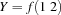• is not entailed by the store, since adding this equality increases the information there, namely by making .

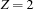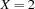• or 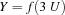are both disentailed since they contradict information already present. They will cause a failure exception to be raised: in the top space this is normally reported to the user in an error message, whereas a subordinated space is merely failed.

12.4 Disjunctions

Now we are in a position to understand the nondeterminate constructs of Oz. Oz provides several disjunctive constructs for nondeterminate choice, also known as don't know choice statements.

12.4.1 or statement

In all the disjunctive statements we are going to use the notion of a clause and a guard. A clause consists of a guard G and a body S1, and has the following form:

G then S1

The guard G has the form:

 X1 ... Xn in S0 

where the variables Xi are existentially quantified with scope extending over both the guard and the body.

The first disjunctive statement has the following form:

or 
   G1 then S1 
[] G2 then S2 
   ... 
[] GN then SN 
end

An or-statement has the following semantics. Assume a thread is executing the statement in space SP.

• The thread is blocked.

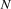• spaces are created 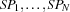with 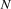new threads executing the guards .

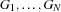• Execution of the father thread remains blocked until at most one of the child spaces is not failed.

• If all children spaces are failed, the parent thread raises a failure condition in its space. This means that if the space of the parent thread is the top space, a failure exception is raised. Otherwise the space is local and it becomes a failed space.

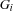
• Only one space remains that is not failed which corresponds to the clause then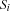 . Assume also that 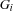has been reduced to the goal 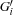and the constraint 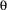. In this case, the space is merged with the parent space. 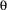and the variables of the store are added to that of the parent store. 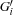executes in its own thread, and the original suspending thread resumes executing the statement 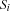. This rule of execution is called unit commit in Oz because execution commits to one alternative disjunct (the only one that is left).

12.4.2 Shorthand Notation

or 
... 
[] Gi 
... 
end

Stands for

or 
... 
[] Gi then skip 
... 
end

Observe that the or statement does not introduce any don't know nondeterminism. A thread executing such a statement waits until things works out in a determinate course of action.

12.4.3 Prolog Comparison

The or statement just described does not have a corresponding construct in Prolog. The Prolog disjunct P ; Q always creates a choice point that is subject to backtracking.

12.5 Determinacy Driven Execution

The or-statement of Oz allows a pure logical form of programming style where computations are synchronized by determinacy conditions. Consider the following program.

proc {Ints N Xs}
   or N = 0 Xs = nil
   [] Xr in  
      N > 0 = true Xs = N|Xr
      {Ints N-1 Xr}
   end  
end 
local  
   proc {Sum3 Xs N R}
      or Xs = nil R = N
      [] X|Xr = Xs in 
         {Sum3 Xr X+N R}
      end 
   end 
in proc {Sum Xs R} {Sum3 Xs 0 R} end 
end 
local N S R in 
   thread {Ints N S} end 
   thread {Sum S {Browse}} end 
   N = 1000
end

The thread executing Ints will suspend until N is known, because it cannot decide on which disjunct to take. Similarly, Sum3 will wait until the list S is known. S will be defined incrementally and that will lead to the suspension and resumption of Sum3. Things will start to take off when the main thread binds N to 1000. This shows clearly that determinacy driven execution gives the synchronization information need to mimic producer/consumer behavior.

12.6 Conditionals

12.6.1 Logical Conditional

A logical conditional is a statement having the following form.

cond X1 ... XN in S0 then S1 else S2 end

where Xi are newly introduced variables, and Si are statements. X1 ... XN in S0 then S1 is the clause of the conditional, and S2 is the alternative.

A cond-statement has the following semantics. Assume a thread is executing the statement in space SP.

• The thread is blocked.

• A space 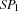is created, with a single thread executing the guard cond X1 ... XN in S0.

• Execution of the father thread remains blocked until 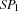is either entailed or disentailed. Notice that these conditions may never occur, e. g. when some thread is suspending or running forever in .

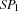• If 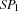is disentailed, the father thread continues with S2.

• If 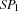is entailed, assume it has been reduced to the store 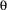and the set of local variables 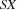In this case, the space is merged with the parent space. 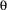and 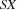added to the parent store, and the father thread continues with the execution of S1.

12.6.2 Prolog Comparison

The cond statement just described corresponds roughly to Prolog's conditional  P -> Q ; R . Oz is a bit more careful about the scope of variables, so local variables Xi have to be introduced explicitly. cond X in P then Q else R end always has the logical semantics 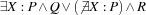, given that we stick to the logical part of Oz. This is not always true in Prolog.

12.6.3 Parallel Conditional

A parallel conditional is of the form

cond G1 then S1 
[] G2 then S2 
... 
else SN end

A parallel conditional is executed by evaluating all conditions G1 ... G(N-1) in an arbitrary order, possibly concurrently, each in its own space. If one of the spaces, say Gi, is entailed, its corresponding statement Si is chosen by the father thread. If all spaces are failed, the else statement SN is chosen, otherwise the executing thread suspends.

Parallel conditionals are useful mostly in concurrent programming, e.g. for programming time-out on certain events. This construct is the basic construct in concurrent logic programming languages (also known as committed-choice languages).

As a typical example from concurrent logic programming let us define the indeterministic binary merge, where the arrival timing of elements on the two streams Xs and Ys determines the order of elements on the resulting stream Zs.

proc {Merge Xs Ys Zs}
   cond 
      Xs = nil then Zs = Ys
   [] Ys = nil then Zs = Xr
   [] X Xr in Xs = X|Xr then Zr in 
      Zs = X|Zr {Merge Xr Ys Zr}
   [] Y Yr in Ys = Y|Yr then Zr in 
      Zs = Y|Zr {Merge Xs Yr Zr}
   end 
end

In general binary-stream merge is inefficient, specially when multiple of these are used to connect multiple threads to a simple server thread. An efficient way to implement a constant-time multi-merge operator is defined below by using cells and streams instread. The procedure {MMerge STs L} has two arguments STs may be either nil, a list of streams to merged, or of the form merge(ST1 ST2) where each STi is again of the same form as STs.

proc {MMerge STs L}
   C = {NewCell L}
   proc {MM STs S E}
      case STs
      of ST|STr then M in 
         thread 
            {ForAll ST proc{$ X} ST1 in {Exchange C X|ST1 ST1} end}
            M=S
         end 
         {MM STr M E}
      [] nil then skip 
      [] merge(STs1 STs2) then M in 
         thread {MM STs1 S M} end 
         {MM STs2 M E}  
      end 
   end 
   E
in 
   thread {MM  STs unit E} end 
   thread if E==unit then L = nil end end 
end

A binary-merge {Merge X Y Z} is simply {MMerge [X Y] Z}.

12.7 Nondeterministic Programs and Search

Oz allows much of the nondeterministic and search-oriented programming as Prolog. This type of programming comes in a little bit different flavour than Prolog. While Prolog comes ready with a default search strategy based on backtracking, Oz allows programmers to devise their suitable search strategies in a way that is separate and orthogonal from the nondeterministic specification of a problem.

To be able to do this Oz has a specific linguistic constructs that create choice point without specifying how they will be explored. A completely separate program can then specify the search strategy.

12.7.1 dis Construct

The following program uses the dis construct of Oz to create a choice point when necessary.

proc {Append Xs Ys Zs}
   dis 
      Xs = nil Ys = Zs then skip 
   [] X Xr Zr in 
      Xs = X|Xr Zs = X|Zr then 
      {Append Xr Ys Zr}
   end 
end

It corresponds roughly to the append/3 program of Prolog:

append([], Ys, Ys). 
append([X|Xr], Ys, [X|Zr]) :- append(Xr, Yr, Zr).

In fact the same kind of abbreviations that hold for or hold also for dis. That is the above program have the following abbreviated form.

proc {Append Xs Ys Zs}
   dis 
      Xs = nil Ys = Zs  
   [] X Xr Zr in 
      Xs = X|Xr Zs = X|Zr then 
      {Append Xr Ys Zr}
   end 
end

Assume the following procedure call:

  
local X in 
   {Append [1 2 3] [a b c] X}
   {Browse X}
end

This will behave exactly as the or construct, i.e. it will deterministically bind X to [1 2 3 a b c]. If we on the other hand try:

local X Y in 
  {Append X Y [1 2 3 a b c]}
  {Browse X#Y}  
end

the bahavior will look the same as with the or construct; the thread executing this sequence of calls will suspend while executing {Append X Y [1 2 3 a b c]}. There is however a difference. The call of Append will create a choice-point with two alternatives:

• X = nil Y = [1 2 3 a b c] then skip

• Xr Xr in 
    X = 1|Xr Zr = [2 3 a b c] then 
    {Append Xr Y Zr}

12.7.2 Define Clause Grammer

Sentence(P) --> NounPhrase(X P1 P) VerbPhrase(X P1)
NounPhrase(X P1 P) --> Determiner(X P2 P1 P) Noun(X P3) RelClause(X P3 P2)  
NounPhrase(X P P) --> Name(X)
VerbPhrase(X P) --> TransVerb(X Y P1) NounPhrase(Y P1 P) | InstransVerb(X P)
RelClause(X P1 and(P1 P2)) --> [that] VerbPhrase(X P2)  
RelClause(_ P P) --> [] 
Determiner(X P1 P2 all(X imp(P1 P2))) --> [every]  
Determiner(X P1 P2 exits(X and(P1 P2))) --> [a]
Noun(X man(X)) --> [man]  
Noun(X woman(X)) --> [woman]
name(john) --> [john]  
name(jan) --> [jan]
TransVerb(X Y loves(X Y)) --> [loves]
IntransVerb(X lives(X))  --> [lives]

proc {Sentence P S0#S}
   X P1 S1 in 
   {NounPhrase X P1 P S0#S1}
   {VerbPhrase X P1 S1#S}
end 
proc {NounPhrase X P1 P S0#S}
   choice 
      P2 P3 S1 S2 in 
      {Determiner X P2 P1 P S0#S1}
      {Noun X P3 S1#S2}
      {RelClause X P3 P2 S2#S}
   [] {Name X S0#S}
      P1 = P
   end 
end 
proc {VerbPhrase X P S0#S}
   choice 
      Y P1 S1 in 
      {TransVerb X Y P1 S0#S1}
      {NounPhrase Y P1 P S1#S}
   [] {IntransVerb X P S0#S}
   end 
end 
proc {TransVerb X Y Z S0#S}
   S0 = loves|S
   Z = loves(X Y)
end 
proc {IntransVerb X Y S0#S}
   S0 = lives|S
   Y = lives(X)
end    
proc {Name X S0#S}
   S0 = X|S
   choice 
      X = john
   [] 
      X = jan
   end 
end 
proc {Noun X Y S0#S}
   choice 
      S0 = man|S
      Y = man(X)
   [] S0 = woman|S
      Y = woman(X)
   end 
end 
proc {Determiner X P1 P2 P S0#S}
   choice 
      S0 = every|S
      P = all(X imp(P1 P2))
   [] S0 = a|S
      P = exists(X and(P1 P2))
   end 
end 
proc {RelClause X P1 P S0#S}
   P2 in 
   choice 
      S1 in 
      S0 = that|S1
      P = and(P1 P2)
      {VerbPhrase X P2 S1#S}
   [] S0 = S
      P = P1
   end 
end 
                  
declare 
proc {Main P}
   {Sentence P [every man that lives loves a woman]#nil}
end

12.7.3 Some Search Procedures

12.7.4 Dis Construct

declare Edge
proc {Connected X Y}
   dis 
      {Edge X Y}  
   [] Z in {Edge X Z}  {Connected Z Y}
   end 
end 
proc {Edge X Y}
   dis 
      X = 1 Y = 2
   [] X = 2 Y = 1
   [] X = 2 Y = 3
   [] X = 3 Y = 4
   [] X = 2 Y = 5
   [] X = 5 Y = 6       
   [] X = 4 Y = 6
   [] X = 6 Y = 7
   [] X = 6 Y = 8
   [] X = 1 Y = 5
   [] X = 5 Y = 1
   end 
end 
 
{ExploreOne
 proc {$ L}
    X Y in 
    X#Y = L {Connected X Y}
 end 
}
{Browse
 {SearchAll
  proc {$ L}
     X Y in 
     X#Y = L {Connected X Y}
  end 
 }}

12.7.5 Negation

proc {NotP P}
   {SearchOne proc {$ L} {P} L=unit end $} = nil
end

proc {ConnectedEnh X Y Visited}
   dis 
      {Edge X Y}
   [] Z in 
      {Edge X Z}
      {NotP proc{$} {Member Z Visited} end}
      {ConnectedEnh Z Y Z|Visited}
   end 
end

12.7.6 Dynamic Predicates

proc {DisMember X Ys}
   dis Ys = X|_ [] Yr in Ys = _|Yr {DisMember X Yr} end 
end

class DataBase from BaseObject 
   attr d
   meth init 
      d := {NewDictionary}
   end 
   meth dic($) @d end 
   meth tell(I)
      case {IsFree I.1} then 
         raise database(nonground(I)) end 
      else 
         Is = {Dictionary.condGet @d I.1 nil} in 
         {Dictionary.put @d I.1 {Append Is [I]}}
      end 
   end 
   meth ask(I)
      case {IsFree I} orelse {IsFree I.1} then 
         {DisMember I {Flatten {Dictionary.items @d}}}
      else 
         {DisMember I {Dictionary.condGet @d I.1 nil}}
      end 
   end 
   meth entries($)
      {Dictionary.entries @d}
   end 
end 
 
declare 
proc {Dynamic ?Pred}
   Pred = {New DataBase init}
end 
proc {Assert P I}
   {P tell(I)}
end 
proc {Query P I}
   {P ask(I)}
end

EdgeP = {Dynamic}
{ForAll
[edge(1 2)
 edge(2 1)   % Cycle
 edge(2 3)
 edge(3 4)
 edge(2 5)
 edge(5 6)      
 edge(4 6)
 edge(6 7)
 edge(6 8)
 edge(1 5)
 edge(5 1)  % Cycle
]
proc {$ I} {Assert EdgeP I} end 
}

12.7.7 The Basic Space Library

12.7.8 Example: A Simple Expert System