8 Programming Patterns
In this chapter, we present a number of patterns that take advantage of concurrency. When programming in Oz, you don't have to agonize over the question whether you really need to invest into a new thread. You just do it! This bears repeating because most people with experience of threads in other languages just don't believe it. Threads aren't just for long running computations: you can spawn threads to perform single operations asynchronously.
In the previous chapter, we demonstrated that it is realistic to create a huge number of threads. However, we exercised the worst case: all threads wanted a piece of the action all the time. In reality, the situation is usually much better: most threads are blocked, waiting for some event, and only a very small number of them compete for processor time.
8.1 Stream Processing Agents
A very common pattern is for a thread to implement an agent that processes all messages that appear on a stream. For example, here, procedure Process is applied to each element of stream Messages, one after the other:
thread {ForAll Messages Process} end Typically, the tail of the stream is uninstantiated, at which point the ForAll procedure, and thus the thread, suspends until a new message comes in that instantiates the stream further.
8.1.1 Stream Merging
As an application of this technique, we consider now the fair merge of two streams L1 and L2 into one single new stream L3. For this, we create the new port Mailbox connected to stream L3, and two agents to forward the messages of L1 and L2 to the Mailbox:
proc {Merge L1 L2 L3}
Mailbox = {Port.new L3}
proc {Forward Msg} {Port.send Mailbox Msg} end
in
thread {ForAll L1 Forward} end
thread {ForAll L2 Forward} end
end Fairness of merging is guaranteed by the fairness of thread scheduling. Actually, the code above can easily be generalized. Here is an abstraction that returns two results: a merged stream L and a procedure AlsoMerge to cause yet another stream to be merged into L:
proc {MakeMerger AlsoMerge L}
Mailbox = {Port.new L}
proc {Forward Msg} {Port.send Mailbox Msg} end
in
proc {AlsoMerge LL}
thread {ForAll LL Forward} end
end
end
8.2 Communication Patterns
A great advantage of concurrency for free is that it gives you a new way to manage design complexity: you can partition your design into a number of small simple agents. You then use streams to connect them together: agents exchange and process messages.
There are two major designs for stream-based communication among agents: one is the email model, the other the newsgroup model. Of course, in realistic applications, you should mix these models as appropriate.
8.2.1 Email Model
In the email model, each agent is equipped with his own mailbox. In the simplest case, the agent is known to others only through its mailbox. For example, here is a function that takes a message processing function as argument, creates an agent, and returns its mailbox:
proc {MakeAgent Process Mailbox}
thread {ForAll {Port.new $ Mailbox} Process} end
end
8.2.2 Newsgroup Model
In the newsgroup model, all agents process and post to the same stream of messages.
Forward Inference Engine: Implementation
We illustrate the newsgroup model with an application to forward inference rules. A forward inference rule has the form 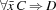 where
where  and
and 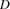 are conjunctions of literals and all variables of the conclusion appear in the premise. The newsgroup will be where inferred literals are published. A rule is said to be partially recognized when some, but not all, of the premise literals have been discovered on the newsgroup. A partially recognized rule is implemented by an agent that reads the newsgroup in search of candidates for the next premise literal. When a rule has been fully recognized, its conclusion is then asserted, which normally results in the publication of new literals.
are conjunctions of literals and all variables of the conclusion appear in the premise. The newsgroup will be where inferred literals are published. A rule is said to be partially recognized when some, but not all, of the premise literals have been discovered on the newsgroup. A partially recognized rule is implemented by an agent that reads the newsgroup in search of candidates for the next premise literal. When a rule has been fully recognized, its conclusion is then asserted, which normally results in the publication of new literals.
We express the engine in the form of a functor that exports the list of Literals being published as well as a procedure to Assert literals and rules.
- <Forward Inference Module>=
functor<Assert conclusion>
import Search
export Literals Assert
define
Literals Box={Port.new Literals}
end
What can be asserted are literals and rules, and conjunctions thereof. A conjunction is represented as a list. Since we don't want to publish twice the same literal (or else we might have termination problems), we maintain here a database of all published literals, indexed according to their outermost predicate. A real implementation might prefer to replace this by an adaptive discrimination tree. Whenever we are about to publish a literal, we first check that it isn't already in the database: in that case, we enter it and then only publish it.
- <Assert conclusion>=
Database = {Dictionary.new}<Assert rule>
proc {Assert Conclusion}
if {IsList Conclusion} then {ForAll Conclusion Assert}
elsecase Conclusion of rule(VarList Premises Conclusion) then
else
Pred = {Label Conclusion}
Lits = {Dictionary.condGet Database Pred nil}
in
if {Member Conclusion Lits} then skip else
{Dictionary.put Database Pred Conclusion|Lits}
{Port.send Box Conclusion}
end
end
end
Asserting a rule consists of creating an agent to recognize it. The agent is equipped with (1) an index (2) a predicate. The index indicates which premise literal to recognize next; it starts from N, the last one, and decreases down to 1. The predicate constrains a representation rule(premises:P conclusion:C) of the partially recognized rule. In order to create this representation, we invoke Abstract to replace the quantified symbolic variables of the rule by new free Oz variables.
- <Assert rule>=
local
N = {Length Premises}
proc {RulePredicate RuleExpression}
case {Abstract VarList Premises#Conclusion} of P#C then
RuleExpression=rule(premises:P conclusion:C)
end
end
in {Agent N RulePredicate} end
Below, we create a mapping from symbolic variables to new free Oz variables, then recursively process the expression to effect the replacements. Note that we cary the list Avoid of symbolic variables that are quantified in a nested rule expression.
- <Replace symbolic by actual variables>=
fun {Abstract VarList E}
Vars = {Record.make o VarList}
fun {Loop E Avoid}
if {IsAtom E} then
if {Member E Avoid} then E
elseif {HasFeature Vars E} then Vars.E
else E end
elseif {IsRecord E} then
case E of rule(VarL Prem Conc) then
rule(VarL {Loop Prem {Append VarL Avoid}}
{Loop Conc {Append VarL Avoid}})
else {Record.map E fun {$ F} {Loop F Avoid} end} end
else E end
end
in {Loop E nil} end
The agent is equipped with the index I of the next premise literal to be recognized and with RulePredicate to constrain the representation of the partially recognized rule. For each literal that is being published, the agent finds all possible solutions that result from unifying it with the Ith premise literal, and produces the corresponding refined predicates. For each new predicate produced, a new agent is created to recognize the next premise literal; unless of course all premise literals have been recognized, in which case we retrieve the corresponding instantiated conclusion and assert it.
- <Agent for partially recognized rule>=
proc {Agent I RulePredicate}
{ForAll Literals
proc {$ Literal}
{ForAll
{Search.allP
proc {$ RuleExpression}
{RulePredicate RuleExpression}
{Nth RuleExpression.premises I}=Literal
end 1 _}
proc {$ NewRulePredicate}
if I==1 then {Assert {NewRulePredicate}.conclusion}
else thread {Agent I-1 NewRulePredicate} end end
end}
end}
end
Forward Inference Engine: Usage
The functor can be compiled as follows:
ozc -c forward.ozand you might experiment with it in the OPI as follows (where DIR is the directory where the compiled functor is located).
declare [Forward] = {Module.link ['DIR/forward.ozf']}
{Browse Forward.literals}
{Forward.assert rule([x y z] [a(x y) a(y z)] a(x z))}
{Forward.assert a(one two)}
{Forward.assert a(two three)}
We asserted one rule expressing the transitivity of binary predicate a, and then two facts. In the browser, you will now observe:
a(one two)|a(two three)|a(one three)|_<Future>8.3 Synchronization
In Oz, synchronization is done on data and typically takes the form of waiting for a variable to become instantiated. Furthermore, this happens automatically: every operation that requires determined data will suspend until this data becomes determined. For example, this is why you can write:
{ForAll Messages Process} where Messages is a stream whose tail only incrementally becomes instantiated with new messages. The ForAll operation suspends when it reaches the uninstantiated tail of the stream, and resumes automatically when further messages become available.
If you need to synchronize explicitly on a variable X, you may write:
{Wait X} which suspends this thread until X becomes determined.
The truth is actually much more general: a conditional suspends until its condition can be decided, one way or the other. What makes this possible is the fact that the information in the constraint store increases monotonically. A conditional suspends until its condition is entailed by the store (implied), or disentailed (its negation is implied). Thus, the Wait operation mentioned above can (almost) be coded as follows:
proc {Wait X}
if X==a then skip else skip end
end This suspends until it can be decided whether or not X is equal to a. I said ``almost'' because in between being free and determined, a variable may be kinded (i. e. its type is known), and the code above does not account for this possibility.
The ForAll procedure is actually implemented as follows:
proc {ForAll L P}
case L of H|T then {P X} {ForAll T P}
elseof nil then skip end
end The case statement (a conditional) suspends until it can be determined whether L matches H|T, i. e. is a list pair.
8.3.1 The Short-Circuit Technique
The short-circuit technique is the standard means of programming an n-way rendez-vous in concurrent constraint programming. The problem is the following: given n concurrent threads, how to synchronize on the fact that they have all terminated? The idea is to have a determined termination token, and to require that each thread, when it terminates, passes the token that it got from its left neighbour to its right neightbour. When the termination token really arrives at the rightmost end, we know that all threads have terminated.
For example, in the example below, we create Token0 with value unit, and then each thread, when it terminates, passes the token on to the next thread. When the value unit reaches Token5, we know that all threads have terminated.
local Token0 Token1 Token2 Token3 Token4 Token5 in
Token0 = unit
thread ... Token1=Token0 end
thread ... Token2=Token1 end
thread ... Token3=Token2 end
thread ... Token4=Token3 end
thread ... Token5=Token4 end
in
%% synchronize on the termination of all 5 threads
{Wait Token5}
endThis technique was used in Section ``Death by Concurrency in Oz''. Of course it can be used for any arbitrary n-way rendez-vous, and not exclusively for synchronizing on the termination of a collection of threads.