2 Type Structure and Description Format
2.1 Type Structure
Types are sets of values of the Oz universe which share a common structure and common operations. Types are divided into primary types and secondary types.
Primary Types
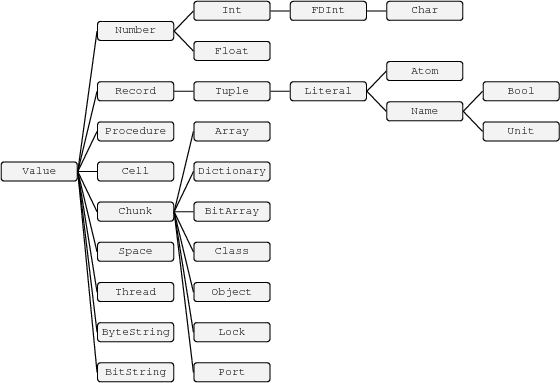
The primary types of Oz are depicted in Figure 2.1. Primary types provide a classification of values in the Oz Universe such that any two different subtypes of some primary type are disjoint. To check for a value to belong to a primary type, only its top-level constructor needs to be tested. Note that implementations of Oz are free to introduce more primary types (so called extensions) as immediate subtypes of either ``value'' or ``chunk''.
Numbers
Numbers are either integers or floats.
Literals
Literals are either atoms or names.
Tuples
Tuples are special records whose features are the integers from 1 to n for some integer n, n >= 0.
Procedures
Procedures are classified according to their arity. We speak about n-ary procedures.
Chunks
Chunks serve to represent abstract data structures. They are defined similarly to records but provide only a restricted set of operations. This makes it possible to hide some or all of their features. Typical chunks are objects and classes, locks and ports, and arrays and dictionaries. There are chunks which do not belong to these types.
Secondary Types
Secondary types are additional types for which Oz provides standard procedures or modules.
Pairs
A pair is a record matching '#'(_ _).
Lists
A list is either the atom nil or a record matching '|'(X Y) (or, equivalently, X|Y) such that Y is again a list. Note that Oz allows cyclic lists which have an infinite unrolling.
Property Lists
A property list is a list of pairs whose first component is a feature, i. e., a literal or an integer.
Virtual Strings
Virtual strings are used to encode strings. Virtual strings contain atoms, strings, byte strings, integers, and floats, and are closed under tuple construction with the label '#'. For more details see Chapter 7.
2.2 Variable Status
Each node X in the store has exactly one of the following statuses: free, determined, future, or kinded.
Free Variable
A variable X is free if the constraint store does not know anything about X apart from variable equalities X = Y.
Determined Variable
A variable X is determined if the constraint store entails X = N for some number N, or if it entails X = f(a1: _ ... an: _) for some label f and the arity [a1 ... an], or if it entails X = Y for some byte string, procedure, cell, chunk, space or thread Y.
Future
A variable X is future if the constraint store entails X = F for some future F.
Kinded Variable
A variable X is kinded if it is neither free nor determined nor future.
2.3 Description Format
Every standard procedure has an associated signature of the form
{Map+Xs+P?Ys}
which specifies its arity, as well as types and modes of its arguments.
Types
The type of an argument is indicated by its name, using the abbreviations summarized in the following table:
Abbreviation | Type |
|---|---|
| atom |
| bool |
| chunk |
| float |
| integer |
| class |
| literal |
| name |
| object |
| procedure |
| record |
| string |
| tuple |
| unit |
| virtual string |
| value |
| number |
| feature |
| atom, float, or int |
| unary procedure or object |
| lists of elements of type |
We use indices such as R1 or R2 to disambiguate several occurrences of arguments of the same type. We combine these abbreviations as in FI meaning ``float or integer'' (i. e., number) or LI meaning ``literal or integer'' (i. e., feature). We use the plural-``s'' suffix to indicate lists of values of a certain type. For instance, Is stands for a list of integers. This suffix can be repeated to indicate lists of lists etc. Additionally, these arguments can be prefixed as in LowI, which indicates that the integer represents a lower bound.
Modes
Modes +, ?, none
The arguments of procedures can have one of four modes which are indicated by a symbol (+, ?, none) attached to the arguments in the signature.
Modes indicate the synchronisation behaviour of a procedure. The application of a procedure P waits until its inputs (+) are determined. If the input arguments are well-typed, P will return outputs (?) of the specified types. Ill-typed input arguments will raise a type error exception. Types may be incompletely checked, especially those of of output arguments: This happens when a value needs not be completely processed to perform an operation, e. g., in List.dropWhile.
Occasionally, signatures of the base language will use the input mode *. Unless one uses any primitives from the constraint extensions, this is identical with +.
Naming Conventions
Aliases
Some of the standard values are so frequent that a special name is provided for them. For example, List.map is also available as Map. The signature of Map occurring in the description of module List (see Section 6.3) says that the procedure List.map is available via the abbreviation Map.
Procedure Names
Given the signature
{procname...}
in the description of the module module, the procedure is available as:
procname, provided procname is just a variable;
module
.procname', where procname' can be obtained from procname by downcasing the first letter and deleting the string module.
For example, the test for lists is available as IsList and as List.is.
Infix Notation
For very frequent procedures like arithmetic operations, there exists a convenient infix notation (see Chapter 11). By convention, the procedure names as they appear in the modules are the infix operators as atoms (i. e., wrapped in quotes). For instance, Number.'+' and Value.'<' have an infix notation using the operators + and <.
A Note on the Examples
Several examples used in this document assume a unary procedure Browse in the environment, which is supposed to display its argument value in a tool called browser.