2.2.2 The Reference of the Implemented Real-Interval Constraint Solver
The module RI is provided as contribution (being part of the Mozart Oz 3 distribution1) and can be accessed either by
declare [RI] = {Module.link ['x-oz://contrib/RI']}or by
import RI at 'x-oz://contrib/RI'as part of a functor definition.
RI.infAn implementation-dependent float value that denotes the smallest possible float number. It is
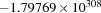 .
. RI.supAn implementation-dependent float value that denotes the smallest possible float number. It is
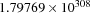 .
. {RI.setPrec+F}Sets the precision of the real-interval constraints to
F.{RI.getLowerBound+RI?F}Returns the lower bound of
RIinF.{RI.getUpperBound+RI?F}Returns the upper bound of
RIinF.{RI.getWidth+RI?F}Returns the width of
RIinF.{RI.var.decl?RI}Constrains
RIto a real-interval constraint with the lower bound to beRI.infand the upper bound to beRI.sup.{RI.var.bounds+L+U?RI}Constrains
RIto a real-interval constraint with the lower bound to beLand the upper bound to beU.{RI.lessEq$X$Y}Imposes the constraint
X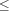
Y.{RI.greater$X$Y}Imposes the constraint
X
Y.{RI.intBounds$RI$D}Imposes the constraint
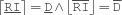 .
. {RI.times$X$Y$Z}Imposes the constraint
X
Y
Z.{RI.plus$X$Y$Z}Imposes the constraint
X+Y
Z.{RI.distribute*RI}Creates a choice-point for
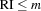 and
and 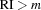 where
where 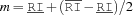 .
.