3.3 The Linear Programming Model
Tackling a multi-knapsack problem with a LP solver amounts to implementing a branch & bound solver to obtain integral solutions. The idea is to compute a continuous solution and to branch over the problem variables with continuous solutions. This is done until only integral problem variables are left. This is what the procedure DistributeKnapSackLP does.
declare
proc {DistributeKnapSackLP Vs ObjFn Constraints MaxProfit}
choice
DupVs = {DuplicateRIs Vs}
DupMaxProfit V DupV
in
DupMaxProfit = {RI.var.bounds
{RI.getLowerBound MaxProfit}
{RI.getUpperBound MaxProfit}}
{LP.solve DupVs ObjFn Constraints DupMaxProfit optimal}
V#DupV = {SelectVar Vs#DupVs}
case {IsDet V} then
DupMaxProfit = MaxProfit
DupVs = Vs
else
choice
{RI.lessEq {Ceil DupV} V}
[]
{RI.lessEq V {Floor DupV}}
end
{DistributeKnapSackLP Vs ObjFn Constraints MaxProfit}
end
end
end
It first duplicates the problem variables (note this is possible due to stability) and invokes the LP solver on them to compute a (possibly continuous) solution. Then it selects the first duplicated continuous problem variable DupV by SelectVar (see below). If continuous variables are left (see the else branch of the case statement), it creates two choices on the corresponding original problem variable V: 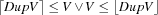 and calls
and calls DistributeKnapSackLP recursively. In case no continuous variables are left, an integral solution is found and the original problem variables are unified with duplicated ones.
For completeness sake the auxiliary functions SelectVar and DuplicateRIs are presented here.
declare | declare |
The procedure KnapsackLP return the script which creates the appropriate parameters for the LP solver and eventually calls DistributeKnapSackLP.
declare
fun {KnapsackLP Problem}
NumProducts = {Length Problem.profit}
Resources = Problem.resources
in
proc {$ Sol}
sol(maxprofit: MaxProfit = {RI.var.decl}
products: Products = {MakeList NumProducts})
= Sol
ObjFn Constraints
in
{ForAll Products proc {$ V}
{RI.var.bounds 0.0 RI.sup V}
end}
ObjFn = objfn(row: {Map Problem.profit IntToFloat}
opt: max)
Constraints =
{Map {Arity Resources}
fun {$ ResourceName}
Resource = Resources.ResourceName
in
constr(row: {Map Resource.npp IntToFloat}
type: '=<'
rhs: {IntToFloat Resource.ta})
end}
{DistributeKnapSackLP Products ObjFn Constraints
MaxProfit}
end
end
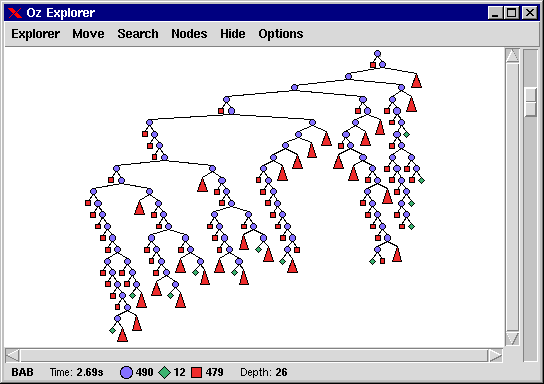
Feeding
{ExploreBest {KnapsackLP Problem}
proc {$ O N}
{RI.lessEq O.maxprofit+1.0 N.maxprofit}
end}produces the following search tree.