3.4 Combining Both Models
Combining both models is simply done by adding the finite domain model without distribution to the linear programming model. The propagator {RI.intBounds F I} is used to connect real-interval constraints with finite domain constraints. It constrains F and I to denote the same integer either as float or as integer, respectively.
declare
fun {KnapsackFDLP Problem}
NumProducts = {Length Problem.profit}
Resources = Problem.resources
in
proc {$ Sol}
sol(maxprofit: FDMaxProfit = {FD.decl}
products: FDProducts = {FD.list NumProducts 0#FD.sup})
= Sol
ObjFn Constraints
MaxProfit = {RI.var.decl}
Products = {MakeList NumProducts}
in
%
% finite domain constraints part
%
FDMaxProfit = {FD.sumC Problem.profit FDProducts '=:'}
{ForAll {Arity Resources}
proc {$ ResourceName}
Resource = Resources.ResourceName
in
{FD.sumC Resource.npp FDProducts '=<:' Resource.ta}
end}
%%
%% linear programming part
%%
{ForAll Products
proc {$ V} {RI.var.bounds 0.0 RI.sup V} end}
ObjFn = objfn(row: {Map Problem.profit {IntToFloat I}}
opt: max)
Constraints =
{Map {Arity Resources}
fun {$ ResourceName}
Resource = Resources.ResourceName
in
constr(row: {Map Resource.npp IntToFloat}
type: '=<'
rhs: {IntToFloat Resource.ta})
end}
%%
%% connecting both constraint systems
%%
{RI.intBounds MaxProfit FDMaxProfit}
{Map Products
proc {$ R D} {RI.intBounds R D} end FDProducts}
{DistributeKnapSackLP Products ObjFn Constraints
MaxProfit}
end
end
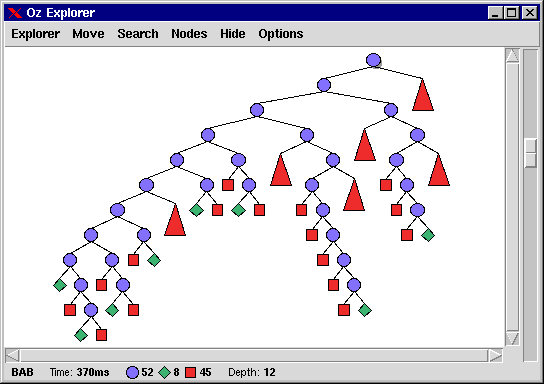
The Oz Explorer produces the following search tree by calling
{ExploreBest {KnapsackFDLP Problem}
proc {$ O N} O.maxprofit <: N.maxprofit end}.