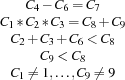3.6 Example: Safe
Problem Specification
The code of Professor Smart's safe is a sequence of 9 distinct nonzero digits 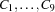 such that the following equations and inequations are satisfied:
such that the following equations and inequations are satisfied:
Can you determine the code?
Model and Distribution Strategy
We choose the obvious model that has a variable for every digit 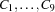 . We distribute over these variables with the standard first-fail strategy.
. We distribute over these variables with the standard first-fail strategy.
proc {Safe C}
{FD.tuple code 9 1#9 C}
{FD.distinct C}
C.4 - C.6 =: C.7
C.1 * C.2 * C.3 =: C.8 + C.9
C.2 + C.3 + C.6 <: C.8
C.9 <: C.8
{For 1 9 1 proc {$ I} C.I \=: I end}
{FD.distribute ff C}
end
Figure 3.5: A script for the Safe Puzzle.
Script
Figure 3.5 shows a script for the Safe Puzzle. The statement
{FD.tuple code 9 1#9 C} constrains the root variable C to a tuple with label code whose components are integers in the domain 1#9. The statement
{For 1 9 1 proc {$ I} C.I \=: I end} posts the constraint 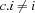 for every
for every 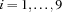 .
.
The full search tree of Safe has 23 nodes and contains the unique solution:
code(4 3 1 8 9 2 6 7 5)