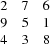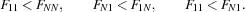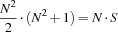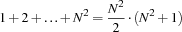7.3 Example: Magic Squares

This example shows a smart representation of a matrix and a concomitant defined constraint of higher order. The model will eliminate symmetries by imposing order constraints. Propagation will be drastically improved by exploiting a redundant constraint.

Problem Specification

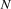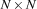The Magic Square Puzzle consists in finding for given an $N\times N$ -matrix such that:

Every field of the matrix is an integer between 1 and .
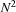The fields of the matrix are pairwise distinct.
The sums of the rows, columns, and the two main diagonals are all equal.

A magic square for 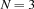N=3 looks as follows:

$\begin{array}{ccc} 2&7&6\\ 9&5&1\\ 4&3&8 \end{array}$

p> The Magic Square Puzzle is extremely hard for large 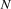. Even for 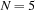{N=5} , our script will have to explore almost 8000 nodes to find a solution.

Model

We model the problem by having a variable 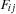$F_{ij}$ for every field 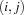(i,j) of the matrix. Moreover, we have one additional variable 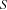and require that the sum of every row, column, and main diagonal equals .

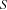Without loss of generality, we can impose the following order constraints eliminating symmetries:

$F_{11}<F_{NN}, \qquad F_{N1}<F_{1N}, \qquad F_{11}<F_{N1}.$

Since the sum of the sums of the rows must equal the sum of all fields, we have the redundant constraint

${N^2\over 2}\cdot(N^2+1) = N\cdot S$

To see this, note that sum of all fields equals

$1+2+\ldots+N^2 = {N^2\over 2}\cdot(N^2+1)$

and that the sum of each of the 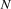rows must be .

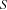Distribution Strategy

We distribute on the variables 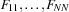$F_{11},\ldots, F_{NN}$ with a first-fail strategy splitting the domain of the selected variable and trying the lower half first.

fun {MagicSquare N}
   NN  = N*N
   L1N = {List.number 1 N 1}  % [1 2 3 ... N]
in 
   proc {$ Square}
      fun {Field I J}
         Square.((I-1)*N + J)
      end 
      proc {Assert F}
         % {F 1} + {F 2} + ... + {F N} =: Sum
         {FD.sum {Map L1N F} '=:' Sum}
      end 
      Sum = {FD.decl}
   in 
      {FD.tuple square NN 1#NN Square}
      {FD.distinct Square}
      %% Diagonals
      {Assert fun {$ I} {Field I I} end}
      {Assert fun {$ I} {Field I N+1-I} end}
      %% Columns
      {For 1 N 1
       proc {$ I} {Assert fun {$ J} {Field I J} end} end}
      %% Rows
      {For 1 N 1
       proc {$ J} {Assert fun {$ I} {Field I J} end} end}
      %% Eliminate symmetries
      {Field 1 1} <: {Field N N}
      {Field N 1} <: {Field 1 N}
      {Field 1 1} <: {Field N 1}
      %% Redundant: sum of all fields = (number rows) * Sum
      NN*(NN+1) div 2 =: N*Sum
      %% 
      {FD.distribute split Square}
   end 
end

Figure 7.3: A script for the Magic Square Puzzle.

Script

Figure 7.3 shows a script realizing the model and distribution strategy just discussed. The actual script is created by a procedure MagicSquare taking N as parameter.

The script represents the matrix as a tuple with 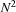N^2 elements. The tuple is the value of the root variable Square. The function

{Field I J}

returns the component of Square that represents the field at position (I,J). The variable Sum takes the sum of the rows, columns, and main diagonals as value. The procedure

{Assert F}

takes a function F and posts the constraint

{F 1} + {F 2} + ... + {F N} = Sum

Obviously, {Assert F} is a defined constraint of higher order. With the help of this defined constraint it is straightforward to state that the sums of the rows, columns, and main diagonals are all equal to Sum.

With the Explorer you can find out that for N=3 there is exactly one magic square satisfying the ordering constraints of our model. Without the ordering constraints there are 8 different solutions. Omitting the propagator for the redundant constraint will increase the search tree by an order of magnitude.