5.7 Generic Propagators

The generic propagators FD.sum, FD.sumC and FD.sumCN do interval propagation. The propagators FD.sumAC and FD.sumACN do interval propagation but may also cut holes into domains. For example,

{FD.dom 0#10 [X Y]} {FD.sumAC [1 ~1] [X Y] '>:' 8}

will reduce the domains of X and Y to 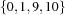$\{0,1,9,10\}$ . Except for propagators FD.sumCN and FD.sumACN, equality is exploited, e. g. {FD.sumC [2 3] [A A] '=:' 10} is equivalent to {FD.sumC [5] [A] '=:' 10}.

$\underline{x}$ , $\overline{x}$

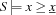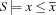Let S denote the current constraint store and x a finite domain integer. $\underline{x}$ denotes the largest integer such that $S \models x \geq \underline{x}$ holds. Analogously, $\overline{x}$ denotes the smallest integer such that $S \models x \leq \overline{x}$ holds.

$\lfloor n \rfloor$, $\lceil n \rceil$

Let n denote a real number. 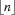$\lfloor n \rfloor$ denotes the largest integer which is equal or smaller than n. Analogously, 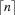$\lceil n \rceil$ denotes the smallest integer which is equal or larger than n.

sum

{FD.sum *Dv +A *D}

creates a propagator for

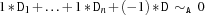
$1*{\tt D}_1+\ldots+1*{\tt D}_n+(-1)*{\tt D}\;\sim_{{\tt A}}\;0$

For the operational semantics see FD.sumC. For the relation symbol '\\=:', the propagator waits until at most one non-determined variable is left. Then the appropriate value is discarded from the variable's domain. For the other relations, the propagator does interval propagation.

sumC

{FD.sumC +Iv *Dv +A *D}

creates a propagator for the scalar product of the vectors Iv and Dv: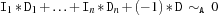

${\tt I}_1*{\tt D}_1+\ldots+{\tt I}_n*{\tt D}_n+(-1)*{\tt D}\;\sim_{{\tt A}}\;0$

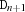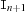Let ${\tt D}_{n+1}$ be D and ${\tt I}_{n+1}$ be -1. Then, the operational semantics is defined as follows. For each product 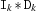${\tt I}_k*{\tt D}_k$ , an isolation (projection) is computed: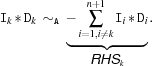

${\tt I}_k*{\tt D}_k \;\sim_{{\tt A}}\; \underbrace{- \sum_{i = 1, i \neq k}^{n+1} {\tt I}_i * {\tt D}_i}_{{\mbox{\sl RHS}}_k}.$

For the right hand side 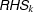${\mbox{\sl RHS}}_k$ , the upper 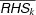$\overline{\mbox{\mbox{\sl RHS}}_k}$ and lower limit 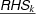$\underline{\mbox{\mbox{\sl RHS}}_k}$ are defined as follows.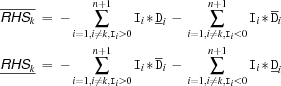

$~$~ \begin{eqnarray*} \overline{\mbox{\mbox{\sl RHS}}_k} \ =\ -\sum_{i =1, i\neq k, {\tt I}_i > 0}^{n+1} {\tt I}_i * \underline{{\tt D}}_i \;-\; \sum_{i =1, i\neq k, {\tt I}_i < 0}^{n+1} {\tt I}_i * \overline{{\tt D}}_i \\ \underline{\mbox{\mbox{\sl RHS}}_k} \ = \ -\sum_{i =1, i\neq k, {\tt I}_i > 0}^{n+1} {\tt I}_i * \overline{{\tt D}}_i \;-\; \sum_{i =1, i\neq k, {\tt I}_i < 0}^{n+1} {\tt I}_i * \underline{{\tt D}}_i \end{eqnarray*} ~$~$

These values are used to narrow the domain of 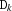${\tt D}_k$ until a fixed point is reached. We describe the propagation for the different possible values of A.

'=<:'

Narrowing is done according to the following inequalities.

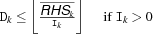
${\tt D}_k \leq \left \lfloor \frac{\overline{{\mbox{\sl RHS}}_k}}{{\tt I}_k} \right \rfloor \quad \mbox{ if\ } {\tt I}_k > 0$

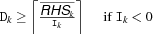
${\tt D}_k \geq \left \lceil \frac{\overline{{\mbox{\sl RHS}}_k}}{{\tt I}_k} \right \rceil \quad \mbox{ if\ } {\tt I}_k < 0$

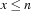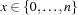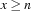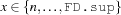Here $x\leq n$ denotes the basic constraint $x \in \{0,\ldots,n\}$ and $x \geq n$ denotes the basic constraint $x \in \{n,\ldots,\codeinline{oz}{FD.sup}\}$ .

The propagator ceases to exist, if the following condition holds.

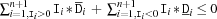
$\sum_{i =1, {\tt I}_i > 0}^{n+1} {\tt I}_i * \overline{{\tt D}}_i \;+\; \sum_{i =1, {\tt I}_i < 0}^{n+1} {\tt I}_i * \underline{{\tt D}}_i \leq 0$

As an example consider

X - Y =<: Z - V

We have the following narrowing.

$\codeinline{oz}{X} \leq \overline{\codeinline{oz}{Z}} - \underline{\codeinline{oz}{V}} + \overline{\codeinline{oz}{Y}} \quad \quad \codeinline{oz}{Y} \geq \underline{\codeinline{oz}{X}} - \overline{\codeinline{oz}{Z}} + \overline{\codeinline{oz}{V}} \quad \quad \codeinline{oz}{Z} \geq \underline{\codeinline{oz}{X}} - \overline{\codeinline{oz}{Y}} + \underline{\codeinline{oz}{V}} \quad\quad \codeinline{oz}{V} \leq \overline{\codeinline{oz}{Z}} - \underline{\codeinline{oz}{X}} + \overline{\codeinline{oz}{Y}}$

The propagator ceases to exist if 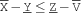$\overline{\codeinline{oz}{X}} - \underline{\codeinline{oz}{Y}} \leq \underline{\codeinline{oz}{Z}} - \overline{\codeinline{oz}{V}}$ holds.

'>=:'

This case can be reduced to =<: due to the observation that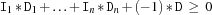

${\tt I}_1*{\tt D}_1+\ldots+{\tt I}_n*{\tt D}_n+(-1)*{\tt D}\;\geq\;0$

is equivalent to

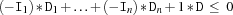
$(-{\tt I}_1)*{\tt D}_1+\ldots+(-{\tt I}_n)*{\tt D}_n+1*{\tt D}\;\leq\;0$

Alternatively, $\underline{\mbox{\mbox{\sl RHS}}_k}$ can be used for the definition.

'<:'

Analogous to '=<:'

'>:'

Analogous to '>=:'

'=:'

In this case, the operational semantics is defined by conjunction of the formulas given for =<: and >=:. Furthermore, coreferences are realized in that, e. g. the propagator 3*X=:3*Y tells the basic constraint X=Y.

'\\=:'

In this case, the propagator waits until at most one non-determined variable is left, say 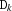${\tt D}_k$ . Then, 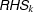${\mbox{\sl RHS}}_k$ denotes a unique integer value which is discarded from the domain of ${\tt D}_k$ .

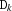Additional propagation is achieved through the realization of coreferences, i. e. equality between variables. If the store S entails (without loss of generality)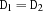 ${\tt D}_1 = {\tt D}_2$ , the generic propagator evolves into: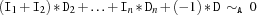

$({\tt I}_1 + {\tt I}_2) * {\tt D}_2 + \ldots + {\tt I}_n*{\tt D}_n+(-1)*{\tt D}\;\sim_{{\tt A}}\;0$

sumCN

{FD.sumCN +Iv *Dvv +A *D}

creates a propagator for

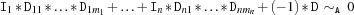
${\tt I}_1*{\tt D}_{11}*\ldots*{\tt D}_{1m_1}+\ldots+{\tt I}_n*{\tt D}_{n1}*\ldots*{\tt D}_{nm_n}+ (-1)*{\tt D}\;\sim_{{\tt A}}\;0$

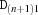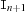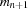Let ${\tt D}_{(n+1)1}$ be D, ${\tt I}_{n+1}$ be -1, and $m_{n+1}$ be 1. Then, the operational semantics is defined as follows. For 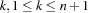$k, 1 \leq k \leq n+1$ , an isolation (projection) is computed: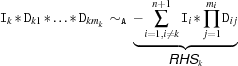

${\tt I}_{k}*{\tt D}_{k1}*\ldots*{\tt D}_{km_k} \;\sim_{{\tt A}}\; \underbrace{- {\sum_{i = 1, i \neq k}^{n+1} {\tt I}_i * \prod_{j=1}^{m_i}{\tt D}_{ij}}}_{{\mbox{\sl RHS}}_k}$

For the right hand side 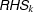${\mbox{\sl RHS}}_k$ , the upper 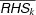$\overline{\mbox{\mbox{\sl RHS}}_k}$ and lower limit 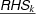$\underline{\mbox{\mbox{\sl RHS}}_k}$ are defined as follows.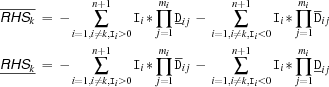

$~$~ \begin{eqnarray*} \overline{\mbox{\mbox{\sl RHS}}_k} \ =\ -\sum_{i =1, i\neq k, {\tt I}_i > 0}^{n+1} {\tt I}_i * \prod_{j=1}^{m_i}\underline{{\tt D}}_{ij} \;-\; \sum_{i =1, i\neq k, {\tt I}_i < 0}^{n+1} {\tt I}_i * \prod_{j=1}^{m_i}\overline{{\tt D}}_{ij} \\ \underline{\mbox{\mbox{\sl RHS}}_k} \ = \ -\sum_{i =1, i\neq k, {\tt I}_i > 0}^{n+1} {\tt I}_i * \prod_{j=1}^{m_i}\overline{{\tt D}}_{ij} \;-\; \sum_{i =1, i\neq k, {\tt I}_i < 0}^{n+1} {\tt I}_i * \prod_{j=1}^{m_i}\underline{{\tt D}}_{ij} \end{eqnarray*} ~$~$

These values are used to narrow the domain of 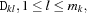${\tt D}_{kl}, 1 \leq l \leq m_k,$ until a fixed point is reached. We describe the propagation for the different possible values of A.

'=<:'

The narrowing is done according to the following inequalities.

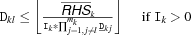
${\tt D}_{kl} \leq \left \lfloor \frac{\overline{\mbox{\sl RHS}}_k}{{\tt I}_k * \prod_{j=1, j\neq l}^{m_k} \underline{{\tt D}}_{kj}} \right \rfloor \quad \mbox{ if\ } {\tt I}_k > 0$

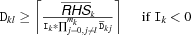
${\tt D}_{kl} \geq \left \lceil \frac{\overline{\mbox{\sl RHS}}_k}{{\tt I}_k * \prod_{j=0, j\neq l}^{m_k} \overline{{\tt D}}_{kj}} \right \rceil \quad \mbox{ if\ } {\tt I}_k < 0$

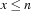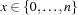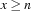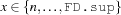Here $x\leq n$ denotes the basic constraint $x \in \{0,\ldots,n\}$ and $x \geq n$ denotes the basic constraint $x \in \{n,\ldots,\codeinline{oz}{FD.sup}\}$ .

The propagator ceases to exist, if the following condition holds.

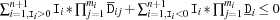
$\sum_{i =1, {\tt I}_i > 0}^{n+1} {\tt I}_i * \prod_{j=1}^{m_i}\overline{{\tt D}}_{ij} + \sum_{i =1, {\tt I}_{i} < 0}^{n+1} {\tt I}_i * \prod_{j=1}^{m_i}\underline{{\tt D}}_i \leq 0$

As an example consider

3*X*Y - Z =<: A

We have the following formulas.

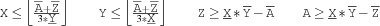
$\codeinline{oz}{X} \leq \left\lfloor \frac{\overline{\codeinline{oz}{A}} + \overline{\codeinline{oz}{Z}}}{3*\underline{\codeinline{oz}{Y}}} \right\rfloor \quad \quad \codeinline{oz}{Y} \leq \left\lfloor \frac{\overline{\codeinline{oz}{A}} + \overline{\codeinline{oz}{Z}}}{3*\underline{\codeinline{oz}{X}}} \right\rfloor \quad \quad \codeinline{oz}{Z} \geq \underline{\codeinline{oz}{X}} *\overline{\codeinline{oz}{Y}} - \overline{\codeinline{oz}{A}} \quad \quad \codeinline{oz}{A} \geq \underline{\codeinline{oz}{X}} *\overline{\codeinline{oz}{Y}} - \overline{\codeinline{oz}{Z}}$

The propagator ceases to exist if 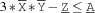$3*\overline{\codeinline{oz}{X}}*\overline{\codeinline{oz}{Y}} - \underline{\codeinline{oz}{Z}} \leq \underline{\codeinline{oz}{A}}$ holds.

'>=:'

This case can be reduced to '=<:' due to the observation that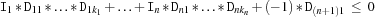

${\tt I}_1*{\tt D}_{11}*\ldots*{\tt D}_{1k_1}+\ldots+{\tt I}_n*{\tt D}_{n1}*\ldots*{\tt D}_{nk_n}+(-1)*{\tt D}_{(n+1)1}\;\leq\;0$

is equivalent to

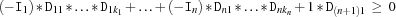
$(-{\tt I}_1)*{\tt D}_{11}*\ldots*{\tt D}_{1k_1}+\ldots+(-{\tt I}_n)*{\tt D}_{n1}*\ldots*{\tt D}_{nk_n}+1*{\tt D}_{(n+1)1}\;\geq\;0$

Alternatively, 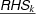$\underline{\mbox{\mbox{\sl RHS}}_k}$ can be used for the definition.

'<:'

Analogous to '=<:'

'>:'

Analogous to '>=:'

'=:'

In this case, the operational semantics is defined by conjunction of the formulas given for '=<:' and '>=:'.

'\\=:'

In this case, the propagator waits until at most one non-determined variable is left, say 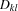$D_{kl}$ . Then, 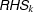${\mbox{\sl RHS}}_k$ denotes a unique integer, and if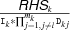

$\frac{{\mbox{\sl RHS}}_k}{{\tt I}_k * \prod_{j=1, j\neq l}^{m_k} {{\tt D}}_{kj}}$

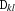denotes an integer value, this value is discarded from the domain of ${\tt D}_{kl}$ .

Coreferences are not exploited for nonlinear generic constraints. The only exception is the expression

X * X =: Y

which has the same operational semantics as {FD.times X X Y} (but note that the occurring variables are not automatically constrained to finite domain integers).

sumAC

{FD.sumAC +Iv *Dv +A *D}

creates a propagator for the absolute value of the scalar product of the vectors Iv and Dv: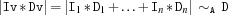

$|{\tt Iv} * {\tt Dv}| = |{\tt I}_1*{\tt D}_1 + \ldots + {\tt I}_n*{\tt D}_n|\;\sim_{{\tt A}}\;{\tt D}$

The operational semantics is as follows. If A is '<:', '=<:' or '\\=:', the following definition holds.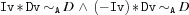

${\tt Iv} * {\tt Dv} \sim_{{\tt A}} D \;\wedge\; (-{\tt Iv})*{\tt Dv} \sim_{{\tt A}} D$

If A is '>:', '>=:' or '=:', the following definition holds.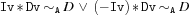

${\tt Iv} * {\tt Dv} \sim_{{\tt A}} D \;\vee\; (-{\tt Iv})*{\tt Dv} \sim_{{\tt A}} D$

where the disjunction is realized by constructive disjunction.

sumACN

{FD.sumACN +Iv *Dvv +A *D}

creates a propagator for

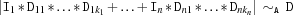
$|{\tt I}_1*{\tt D}_{11}*\ldots*{\tt D}_{1k_1}+\ldots+{\tt I}_n*{\tt D}_{n1}*\ldots*{\tt D}_{nk_n}|\;\sim_{{\tt A}}\;{\tt D}$

The operational semantics is defined analogously to FD.sumAC.

sumD

{FD.sumD *Dv +A *D}

creates a propagator analogous to FD.sum but performs domain-consistent propagation. Note that only equality (A is '=:') and disequality (A is '\\=:') are supported, as for inequalities domain and bounds propagation are equivalent.

sumCD

{FD.sumCD +Iv *Dv +A *D}

creates a propagator analogous to FD.sumC but performs domain-consistent propagation. Note that only equality (A is '=:') and disequality (A is '\\=:') are supported, as for inequalities domain and bounds propagation are equivalent.