5.8 Symbolic Propagators

The following propagators do domain propagation or amplify the store by constraints X::Spec, where Spec may also contain holes.

distinct

{FD.distinct *Dv}

All elements in Dv are pairwise distinct. If one element becomes determined, the remaining elements are constrained to be different from it. If two variables become equal, the propagator fails, e. g. {FD.distinct [A A B]} will fail even if A is not determined.

distinctB

{FD.distinctB *Dv}

All elements in Dv are pairwise distinct. Uses bounds propagation, but does not use value propagation as FD.distinct. Also fails, if two variables are equal. Currently uses the quadratic algorithm for propagation by Puget described in [Pug98].

distinctD

{FD.distinctD *Dv}

All elements in Dv are pairwise distinct. Uses full domain propagation. Also fails, if two variables are equal. Is based on Régin's algorithm [Rég94].

distinctOffset

{FD.distinctOffset *Dv +Iv}

All sums 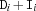are pairwise distinct, i. e. for all 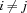holds 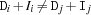. If one 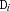becomes determined, the remaining elements 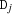are constrained to be different from .

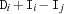distinct2

{FD.distinct2 *Dv1 +Iv1 *Dv2 +Iv2}

Assume that all arguments are tuples of width n. Then the propagator's operational semantics is defined as follows.

or Dv1.i + IV1.i =<: Dv1.j 
[] Dv1.j + IV1.j =<: Dv1.i 
[] Dv2.i + IV2.i =<: Dv2.j 
[] Dv2.j + IV2.j =<: Dv2.i 
end

This propagator may be used to express that a number of rectangles must not overlap in the two-dimensional space. In this case Dv1 and Dv2 may denote the x-coordinates and y-coordinates of the lower left corner of the rectangles, respectively. Iv1 and Iv2 may denote the widths and heights of the rectangles, respectively.

atMost

{FD.atMost *D *Dv +I}

atLeast

{FD.atLeast *D *Dv +I}

exactly

{FD.exactly *D *Dv +I}

At most, at least, exactly D elements of Dv are equal to I. The operational semantics is defined as follows. Let VFoldL be either FoldL or Record.foldL depending on the type of Dv and

S = {VFoldL Dv fun{$ In D1} {FD.plus In D1=:I} end 0}

The propagator FD.atMost, FD.atLeast and FD.exactly are defined by D>=:S, D=<:S and D=:S, respectively.

element

{FD.element *D1 +Iv *D2}

The D1-th element of Iv is D2.

It propagates as follows. For each integer i in the domain of D1, the i-th element of Iv is in the domain of D2; and no other values. For each value j in the domain of D2, all positions where j occurs in Is are in the domain of D1; and no other values. For example,

{FD.int [1 3] X} {FD.element X [5 6 7 8] Y}

will constrain Y to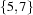 . D1 is constrained to be greater than 0.