5.9 0/1 Propagators
Using the mapping from 0 and 1 to the truth values false and true, respectively, logical connectives between finite domain integers are defined. If at most one argument is a free variable, it will be constrained to a finite domain integer in 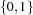 . Such a finite domain integer is also called a 0/1-integer. The propagators exploit equality and may also post equality between variables.
. Such a finite domain integer is also called a 0/1-integer. The propagators exploit equality and may also post equality between variables.
The operational semantics is detailed only for FD.conj. For the remaining propagators, the operational semantics is defined accordingly, exploiting as much information as possible (including coreferences).
-
conj {FD.conj$D1$D2$D3}D3is the conjunction ofD1andD2. The operational semantics can be described by the following code[D1 D2 D3] ::: 0#1
cond D1=0 then D3=0
[] D1=1 then D2=D3
[] D2=0 then D3=0
[] D2=1 then D1=D3
[] D3=1 then D1=1 D2=1
[] D1=D2 then D1=D3
end-
disj {FD.disj$D1$D2$D3}D3is the disjunction ofD1andD2.-
exor {FD.exor$D1$D2$D3}D3is the exclusive disjunction ofD1andD2.-
nega {FD.nega$D1$D2}D2is the negation ofD1.-
impl {FD.impl$D1$D2$D3}D3is the implication ofD2byD1(``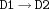 '').
''). -
equi {FD.equi$D1$D2$D3}D3is the equivalence ofD1byD2(``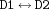 '').
'').