5.10 Reified Constraints

Reified constraints reflect the validity of a constraint C into a 0/1-valued finite domain integer. The propagator realizing a reified constraint is called the reification propagator. The reification propagators wait in the same way as their non-reified counterparts. All reification propagators constrain their last argument to a 0/1-valued finite domain integer.

Let C be a constraint and P the corresponding propagator. Reifying C into a 0/1-valued variable D is defined by

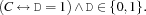
This is implemented by

D::0#1  
or P D=1
[] P^N D=0
end

Here, 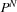denotes the negation of P (i. e. a propagator for the negation of the denotational semantics of P).

If P is one of {FD.reified.int Spec X} and {FD.reified.dom Spec Xv}, then 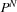denotes {FD.reified.int ComplSpec X} and {FD.reified.dom ComplSpec Xv}, respectively (where ComplSpec = compl(Spec) if Spec is a simple domain specification, and ComplSpec = SSpec if Spec = compl(SSpec)).

For the propagators P wich are parameterized by a relation symbol A, the symbol of the negated relation occurs in 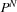. For instance, if P is {FD.sum Ds '<:' X Y}, then 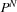is {FD.sum Ds '>=:' X Y}.

reified.int

{FD.reified.int +Spec *D1 D2}

reifies {FD.int Spec D1} into D2.

reified.dom

{FD.reified.dom +Spec Dv D}

reifies {FD.dom Spec Dv} into D.

reified.sum

{FD.reified.sum *Dv +A *D1 D2}

reifies {FD.sum Dv A D1} into D2.

reified.sumC

{FD.reified.sumC +Iv *Dv +A *D1 D2}

reifies {FD.sumC Iv Dv A D1} into D2.

reified.sumCN

{FD.reified.sumCN +Iv *Dvv +A *D1 D2} 

reifies {FD.sumCN Iv Dvv A D1} into D2.

reified.sumAC

{FD.reified.sumAC +Iv *Dv +A *D1 D2}

reifies {FD.sumAC Iv Dv A D1} into D2.

reified.sumACN

{FD.reified.sumACN +Iv *Dvv +A *D1 D2} 

reifies {FD.sumACN Iv Dvv A D1} into D2.

reified.distance

{FD.reified.distance *D1 *D2 +A *D3 D4}

reifies {FD.distance D1 D2 A D3} into D4.

reified.card

{FD.reified.card *D1 *Dv *D2 D3}

Dv is a vector of Boolean variables. FD.reified.card creates a propagator for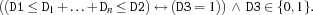

which reifies into D3 the conjunction

D1 =<: D1 + ... + Dn
D1 + ... + Dn =<: D2 

More specifically, its operational semantics is defined through

D3 :: 0#1
or D1 =<: D1 + ... + Dn  
   D1 + ... + Dn =<: D2
   D3 = 1
[] or D1 >: D1 + ... + Dn  
   [] D1 + ... + Dn >: D2
   end 
   D3 = 0
end