7.1 Finite Set Intervals

inf: FS.inf; An integer constant that denotes the smallest possible element of a set. Its value is implementation-dependent. In Mozart FS.inf is 0.
sup: FS.sup; An integer constant that denotes the greatest possible element of a set. Its value is implementation-dependent. In Mozart FS.sup is 134 217 726.
compl: {FS.compl $M1 $M2}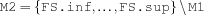; $\codeinline{oz}{M2} = \{\codeinline{oz}{FS.inf},\ldots,\codeinline{oz}{FS.sup}\}\setminus \codeinline{oz}{M1}$
complIn: {FS.complIn $M1 $M2 $M3}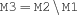; $\codeinline{oz}{M3} = \codeinline{oz}{M2} \setminus \codeinline{oz}{M1}$
include: {FS.include +D *M}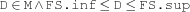; $\codeinline{oz}{D} \in \codeinline{oz}{M} \wedge \codeinline{oz}{FS.inf} \le \codeinline{oz}{D} \le \codeinline{oz}{FS.sup}$
exclude: {FS.exclude +D *M}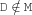; $\codeinline{oz}{D} \notin \codeinline{oz}{M}$
card: {FS.card *M ?D}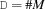; $\codeinline{oz}{D} = \# {M}$
cardRange: {FS.cardRange +I1 +I2 *M}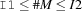; $\codeinline{oz}{I1} \le \# {M} \le {I2}$
isIn: {FS.isIn +I *M ?B}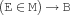; $(\codeinline{oz}{E} \in \codeinline{oz}{M}) \rightarrow \codeinline{oz}{B}$
makeWeights: {FS.makeWeights +SpecW ?P}; Returns a procedure with signature {P +I1 ?I2}. This procedure maps an element to a weight according to the weight description passed to FS.makeWeights.