7 Finite Set Constraints: `FS`

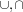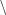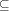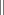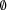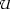We use the following notation for operations and relations on sets. We write $\cup, \cap$ , and $\backslash$ for set union, intersection, and difference, $\subseteq$ and $\|$ for inclusion and disjointness, $\#$ for the set cardinality, and $\in$ for the element relation. Furthermore, we write $\emptyset$ and $\uniset$ for the empty set and the universal set.

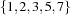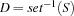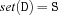For every set specification Spec we write the set M specified by Spec as M = $~$ \newcommand{\sic}[2]{\mbox{$[#1,#2]$}} \newcommand{\conv}{{\it set}} \newcommand{\convinv}{{\it set}^{-1}} ~$~ \conv({Spec})$ . For example, $\conv(\mbox{\codeinline{oz}{[1\#3 5 7]}})$ denotes $\{1,2,3,5,7\}$ . Further, for every set S we denote with ${D} = \convinv({S})$ a set description D such that $\conv({\tt D}) = {\tt S}$ .

For more information on the finite set constraint system see [MM97].

7.1 Finite Set Intervals

7.2 Sets over Integers

7.3 Standard Propagators

7.4 Finite Set Interval Variables

7.5 Finite Set Constants

7.6 Reified Propagators

7.7 Iterating and Monitoring

7.8 Reflection

7.9 Distribution

7 Finite Set Constraints: FS

7 Finite Set Constraints: `FS`