7.3 Standard Propagators

diff

{FS.diff $M1 $M2 $M3}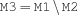

intersect

{FS.intersect $M1 $M2 $M3}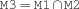

intersectN

{FS.intersectN *Mv *M}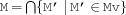

union

{FS.union $M1 $M2 $M3}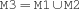

unionN

{FS.unionN $Mv $M}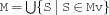

subset

{FS.subset $M1 $M2}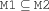

disjoint

{FS.disjoint $M1 $M2}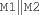

disjointN

{FS.disjointN *Mv}

All elements of the vector Mv are pairwise disjoint.

distinct

{FS.distinct $M1 $M2}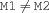

distinctN

{FS.distinctN *MV}

All elements of the vector Mv are pairwise distinct.

partition

{FS.partition $MV $M}

Mv is a partition of M; that is, Mv contains pairwise disjoint sets such that their union yields M.