3 Basics
We will initially restrict ourselves to the sequential programming style of Oz. At this stage you may think of Oz computations as performed by a sequential process that executes one statement after the other. We call this process a thread. This thread has access to the store. It is able to manipulate the store by reading, adding, and updating information stored in the store. Information is accessed through the notion of variables. A thread can access information only through the variables visible to it, directly or indirectly. Oz variables are single-assignment variables or more appropriately logic variables. In imperative languages like C and Java, a variable can be assigned multiple times. In contrast, single assignment variables can be assigned only once. This notion is known from many languages including dataflow languages and concurrent logic programming languages. A single assignment variable has a number of phases in its lifetime. Initially it is introduced with unknown value, and later it might be assigned a value, in which case the variable becomes bound. Once a variable is bound, it cannot itself be changed. A logic variable is a single assignment variable that can also be equated with another variable. Using logic variables does not mean that you cannot model state-change because a variable, as you will see later, could be bound to a cell, which is stateful, i.e., the content of a cell can be changed.
A thread executing the statement:
local X Y Z in S end
will introduce three single assignment variables X, Y, Z and execute the statement S in the scope of these variables. A variable normally starts with an upper-case letter, possibly followed by an arbitrary number of alphanumeric characters. Variables may also be presented textually as any string of printable characters enclosed within back-quote characters, e.g. `this $ is a variable`. Before the execution of S the variables declared will not have any associated values. We say that the variables are unbound. Any variable in an Oz program must be introduced, except for certain pattern matching constructs to be shown later.
Another form of declaration is:
declare X Y Z in S
This is an open-ended declaration that makes X, Y, and Z visible globally in S, as well as in all statements that follow S textually, unless overridden again by another variable declaration of the same textual variables. X, Y, Z are global variables.
3.1 Primary Oz Types
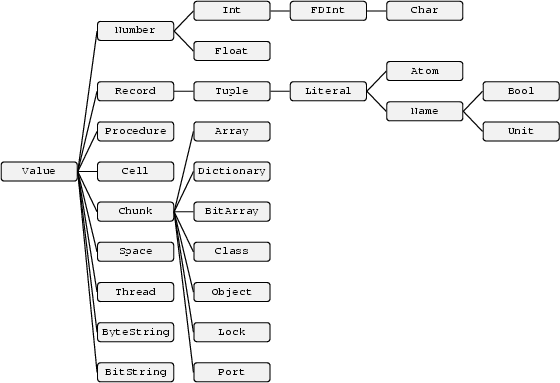
Oz is a dynamically typed language. Figure 3.1 shows the type hierarchy of Oz. Any variable, if it ever gets a value, will be bound to a value of one of these types. Most of the types seem familiar to experienced programmers, except probably Chunk, Cell, Space, FDInt and Name. We will discuss all of these types in due course. For the impatient reader here are some hints. The Chunk data type allows users to introduce new abstract data types. Cell introduces the primitive notion of state-container and state modification. Space will be needed for advanced problem solving using search techniques. FDInt is the type of finite domain that is used frequently in constraint programming, and constraint satisfaction. Name introduces anonymous unique unforgeable tokens.
The language is dynamically-typed in the sense that when a variable is introduced, its type as well as its value are unknown. Only when the variable is bound to an Oz value, does its type become determined.
3.2 Adding Information
In Oz, there are few ways of adding information to the store or (said differently) of binding a variable to a value. The most common form is using the equality infix operator =. For example, given that the variable X is declared the following statement:
X = 1
will bind the unbound variable X to the integer 1, and add this information to the store. Now, if X is already assigned the value 1, the operation is considered as performing a test on X. If X is already bound to an incompatible value, i.e. to any other value different from 1, a proper exception will be raised. Exception handling is described later.
3.3 Data Types with Structural Equality
The hierarchy starting from Number and Record in Figure 3.1 defines the data types of Oz whose members (values) are equal only if they are structurally similar. For example two numbers are equal if they have the same type, or one is a subtype of the other, and have the same value. For example, if both are integers and are identical numbers or both are lists and their head elements are identical as well as their respective tail lists. Structural equality allows values to be equivalent even if they are replicas occupying different physical memory location.
3.4 Numbers
The following program, introduces three variables I,F and C. It assigns I an integer, F a float, and C the character t in this order. It then displays the list consisting of I,F, and C.
local I F C in
I = 5
F = 5.5
C = &t
{Browse [I F C]}
end
Oz supports binary, octal, decimal and hexadecimal notation for integers, which can be arbitrary large. An octal starts with a leading 0, and a hexadecimal starts with a leading 0x or 0X. Floats are different from integers and must have decimal points. Other examples of floats are shown where ~ is unary minus:
~3.141 4.5E3 ~12.0e~2
In Oz, there is no automatic type conversion, so 5.0 = 5 will raise an exception. Of course, there are primitive procedures for explicit type conversion. These and many others can be found in [Shu98]. Characters are a subtype of integers in the range of 0, ..., 255. The standard ISO 8859-1 coding is used (not Unicode). Printable characters have external representation, e.g. &0 is actually the integer 48, and &a is 97. Some control characters have also a representation e.g. &\n is a new line. All characters can be written as &\ooo, where o is an octal digit.
Operations on characters, integers, and floats can be found in the library modules Char, Float, and Int. Additional generic operations on all numbers are found in the module Number.
3.5 Literals
Another important category of atomic types, i.e. types whose members have no internal structure, is the category of literals. Literals are divided into atoms and names. An Atom is symbolic entity that has an identity made up of a sequence of alphanumeric characters starting with a lower case letter, or arbitrary printable characters enclosed in quotes. For example:
a foo '=' ':=' 'OZ 3.0' 'Hello World'
Atoms have an ordering based on lexicographic ordering.
Another category of elementary entities is Name. The only way to create a name is by calling the procedure {NewName X} where X is assigned a new name that is guaranteed to be worldwide unique. Names cannot be forged or printed. As will be seen later, names play an important role in the security of Oz programs. A subtype of Name is Bool, which consists of two names protected from being redefined by having the reserved keywords true and false. Thus a user program cannot redefine them, and mess up all programs relying on their definition. There is also the type Unit that consists of the single name unit. This is used as synchronization token in many concurrent programs.
local X Y B in
X = foo
{NewName Y}
B = true
{Browse [X Y B]}
end
3.6 Records and Tuples
Records are structured compound entities. A record has a label and a fixed number of components or arguments. There are also records with a variable number of arguments that are called open records. For now, we restrict ourselves to 'closed' records. The following is a record:
tree(key: I value: Y left: LT right: RT)
It has four arguments, and the label tree. Each argument consists of a pair Feature:Field, so the features of the above record are key, value, left, and right. The corresponding fields are the variables I,Y,LT, and RT. It is possible to omit the features of a record reducing it to what is known from logic programming as a compound term. In Oz, this is called a tuple. So, the following tuple has the same label and fields as the above record:
tree(I Y LT RT)
It is just a syntactic notation for the record:
tree(1:I 2:Y 3:LT 4:RT)
where the features are integers starting from 1 up to the number of fields in the tuple. The following program will display a list consisting of two elements one is a record, and the other is tuple having the same label and fields:
declare T I Y LT RT W in
T = tree(key:I value:Y left:LT right:RT)
I = seif
Y = 43
LT = nil
RT = nil
W = tree(I Y LT RT)
{Browse [T W]}
The display will show:
[tree(key:seif value:43 left:nil right:nil)
tree(seif 43 nil nil)]
3.7 Operations on records
We discuss some basic operations on records. Most operations are found in the module Record. To select a field of a record component, we use the infix dot operator, e. g. Record.Feature
% Selecting a Component
{Browse T.key}
{Browse W.1}
% will show seif twice in the browser
seif
seif
The arity of a record is a list of the features of the record sorted lexicographically. To display the arity of a record we use the procedure Arity. The procedure application {Arity R X} will execute once R is bound to a record, and will bind X to the arity of the record. Executing the following statements
% Getting the Arity of a Record
local X in {Arity T X} {Browse X} end
local X in {Arity W X} {Browse X} end
will display
[key left right value]
[1 2 3 4]
Another useful operation is conditionally selecting a field of a record. The operation CondSelect takes a record R, a feature F, and a default field-value D, and a result argument X. If the feature F exists in R, X is bound to R.F, otherwise X is bound to the default value D. CondSelect is not really a primitive operation. It is definable in Oz. The following statements:
% Selecting a component conditionally
local X in {CondSelect W key eeva X} {Browse X} end
local X in {CondSelect T key eeva X} {Browse X} end
will display
eeva
seif
A common infix tuple-operator used in Oz is #. So, 1#2 is a tuple of two elements, and observe that 1#2#3 is a single tuple of three elements:
'#'(1 2 3)
and not the pair 1#(2#3). With the # operator, you cannot directly write an empty or a single element tuple. Instead, you must fall back on the usual prefix record syntax: the empty tuple must be written '#'() or just '#', and a single element tuple '#'(X).
The operation {AdjoinAt R1 F X R2} binds R2 to the record resulting from adjoining the field X to R1 at feature F. If R1 already has the feature F, the resulting record R2 is identical to R1 except for the field R1.F whose value becomes X. Otherwise the argument F:X is added to R1 resulting in R2.
The operation {AdjoinList R LP S} takes a record R, a list of feature-field pairs, and returns in S a new record such that:
The label of R is equal to the label of S.
S has the components that are specified in LP in addition to all components in R that do not have a feature occurring in LP.
This operation is of course defined by using AdjointAt.
local S in
{AdjoinList tree(a:1 b:2) [a#3 c#4] S}
{Show S}
end
% gives S=tree(a:3 b:2 c:4)
3.8 Lists
As in many other symbolic programming languages, e.g. Scheme and Prolog, lists form an important class of data structures in Oz. The category of lists does not belong to a single data type in Oz. They are rather a conceptual structure. A list is either the atom nil representing the empty list, or is a tuple using the infix operator | and two arguments which are respectively the head and the tail of the list. Thus, a list of the first three positive integers is represented as:
1|2|3|nil
Another convenient special notation for a closed list, i. e. a list with a determined number of elements is:
[1 2 3]
The above notation is used only for closed list, so a list whose first two elements are 1 and 2, but whose tail is the variable X looks like:
1|2|X
One can also use the standard record notation for lists:
'|'(1 '|'(2 X))
Further notational variant is allowed for lists whose elements correspond to character codes. Lists written in this notation are called strings, e.g.
"OZ 3.0"
is the list
[79 90 32 51 46 48]
or equivalently
[&O &Z & &3 &. &0]
3.9 Virtual Strings
A virtual string is a special tuple that represents a string with virtual concatenation, i.e. the concatenation is performed when really needed. Virtual strings are used for I/O with files, sockets, and windows. All atoms, except nil and '#', as well as numbers, strings, or '#'-labeled tuples can be used to compose virtual strings. Here is one example:
123#"-"#23#" is "#100
represents the string
"123-23 is 100"
Warning:For each data type discussed in section, there is a corresponding module in the Mozart system. The modules define operations on the corresponding data type. You may find more about these operations in The Oz Base Environment documentation