6.1 Example: Coloring a Map
Problem Specification
Given a map showing the West European countries Netherlands, Belgium, France, Spain, Portugal, Germany, Luxemburg, Switzerland, Austria, and Italy, find a coloring such that neighboring countries have different color and a minimal number of colors is used.
Model
We have a variable 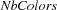 saying how many different colors we can use. Moreover, we have a variable for every country. For every pair
saying how many different colors we can use. Moreover, we have a variable for every country. For every pair  ,
,  of countries having a border in common we impose the constraint
of countries having a border in common we impose the constraint 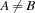 . We represent colors as numbers. Hence we constrain all variables for countries to integers in
. We represent colors as numbers. Hence we constrain all variables for countries to integers in 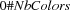 .
.
Distribution Strategy
We first distribute on 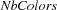 , trying the numbers
, trying the numbers 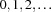 in ascending order. After
in ascending order. After  is determined, we distribute on the variables for the countries using the usual first-fail strategy.
is determined, we distribute on the variables for the countries using the usual first-fail strategy.
fun {MapColoring Data}
Countries = {Map Data fun {$ C#_} C end}
in
proc {$ Color}
NbColors = {FD.decl}
in
{FD.distribute naive [NbColors]}
%% Color: Countries --> 1#NbColors
{FD.record color Countries 1#NbColors Color}
{ForAll Data
proc {$ A#Bs}
{ForAll Bs proc {$ B} Color.A \=: Color.B end}
end}
{FD.distribute ff Color}
end
end
Data = [ austria # [italy switzerland germany]
belgium # [france netherlands germany luxemburg]
france # [spain luxemburg italy]
germany # [austria france luxemburg netherlands]
italy # nil
luxemburg # nil
netherlands # nil
portugal # nil
spain # [portugal]
switzerland # [italy france germany austria] ]
Figure 6.1: A script for the Map Coloring Problem together with a data specification.
Script
The script appears in Figure 6.1. It is parameterized with the specification of the map to be colored. The figure shows the specification of a map containing some European countries.
The script first creates a local variable NbColors that specifies the number of different colors to be used for coloring the map. Then it distributes naively on NbColors. Recall that a distributor blocks its thread until it has done its job. After NbColors is determined by distribution, the variable Color is constrained to a record mapping the country names to integers in 1#NbColors. This implicitly creates the variables for the Countries. Next the script creates a propagator
Color.A \=: Color.B for every pair A, B of bordering countries. Finally, the script distributes on Color using the first-fail strategy.
The statement
{ExploreOne {MapColoring Data}}will show the search tree explored to find the first solution, which looks as follows:
color(
austria: 1 belgium: 3 france: 1
germany: 2 italy: 2 luxemburg: 4
netherlands: 1 portugal: 1 spain: 2
switzerland: 3
) The search tree of MapColoring is interesting. First, colorings with 0, 1, 2 and 3 colors are searched and not found. Then a coloring with 4 colors is searched. Now a solution is found quickly, without going through further failure nodes. There are many solutions using 4 colors since the particular color given to a country does not matter.