6.2 Example: Conference
This example will employ the constraint provided by FD.atMost.
Problem Specification
We want to construct the time table of a conference. The conference will consist of 11 sessions of equal length. The time table is to be organized as a sequence of slots, where a slot can take up to 3 parallel sessions. There are the following constraints on the timing of the sessions:
Session 4 must take place before Session 11.
Session 5 must take place before Session 10.
Session 6 must take place before Session 11.
Session 1 must not be in parallel with Sessions 2, 3, 5, 7, 8, and 10.
Session 2 must not be in parallel with Sessions 3, 4, 7, 8, 9, and 11.
Session 3 must not be in parallel with Sessions 5, 6, and 8.
Session 4 must not be in parallel with Sessions 6, 8, and 10.
Session 6 must not be in parallel with Sessions 7 and 10.
Session 7 must not be in parallel with Sessions 8 and 9.
Session 8 must not be in parallel with Session 10.
The time table should minimize the number of slots.
Model
The model has a variable 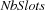 saying how many slots the conference has. For the given data,
saying how many slots the conference has. For the given data, 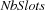 can be constrained to the finite domain
can be constrained to the finite domain  . The model also has a variable
. The model also has a variable 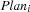 for every session
for every session  , where
, where 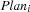 stands for the number of the slot in which Session
stands for the number of the slot in which Session  will take place. Every variable
will take place. Every variable 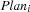 can be constrained to the finite domain
can be constrained to the finite domain 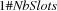 . The remaining constraints are obvious from the problem description.
. The remaining constraints are obvious from the problem description.
Distribution Strategy
We use a two-dimensional distribution strategy. We first distribute on 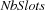 , trying smaller values first. Once
, trying smaller values first. Once 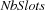 is determined, we distribute on the variables
is determined, we distribute on the variables 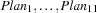 using the standard first-fail strategy.
using the standard first-fail strategy.
fun {Conference Data}
NbSessions = Data.nbSessions
NbParSessions = Data.nbParSessions
Constraints = Data.constraints
MinNbSlots = NbSessions div NbParSessions
in
proc {$ Plan}
NbSlots = {FD.int MinNbSlots#NbSessions}
in
{FD.distribute naive [NbSlots]}
%% Plan: Session --> Slot
{FD.tuple plan NbSessions 1#NbSlots Plan}
%% at most NbParSessions per slot
{For 1 NbSlots 1
proc {$ Slot} {FD.atMost NbParSessions Plan Slot} end}
%% impose constraints
{ForAll Constraints
proc {$ C}
case C
of before(X Y) then
Plan.X <: Plan.Y
[] disjoint(X Ys) then
{ForAll Ys proc {$ Y} Plan.X \=: Plan.Y end}
end
end}
{FD.distribute ff Plan}
end
end
Data = data(nbSessions:11 nbParSessions:3
constraints: [ before(4 11) before(5 10) before(6 11)
disjoint(1 [2 3 5 7 8 10])
disjoint(2 [3 4 7 8 9 11])
disjoint(3 [5 6 8]) disjoint(4 [6 8 10])
disjoint(6 [7 10]) disjoint(7 [8 9])
disjoint(8 [10]) ] )
Figure 6.2: A script for conference scheduling together with a data specification.
Script
The script in Figure 6.2 is parameterized with an argument Data specifying the conference to be organized. The figure also shows the specification of the conference described in the problem specification.
The script creates a local variable NbSlots specifying the number of slots used by the conference. It then distributes naively on NbSlots. After NbSlots is determined, it constrains its root variable Plan to a tuple mapping the session numbers 1, ..., 11 to integers in 1#NbSlots. This implicitly creates variables corresponding to the variables 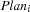 of the model.
of the model.
The statement
{FD.atMost NbParSessions Plan Slot} creates a propagator for a constraint saying that at most NbParSessions components of Plan can be equal to Slot.
The statement {ForAll Constraints ... } imposes the constraints of the conference to be scheduled.
The last statement distributes on Plan using the first-fail strategy.
The statement
{ExploreOne {Conference Data}}will explore the search tree until the first solution is found. The first solution minimizes the number of slots and looks as follows:
plan(1 2 3 1 2 2 3 4 1 3 4)This plan says that the conference requires 4 slots, where the sessions 1, 4 and 9 take place in slot 1, the sessions 2, 5 and 6 take place in slot 2, the sessions 3, 7 and 10 take place in slot 3, and the sessions 8 and 11 take place in slot 4.