5 A Crew Allocation Problem
Problem Specification
A small air-line has to assign their 20 flight attendants to 10 flights. Each flight has to be accompanied by a certain number of cabin crew (see Table 5.1) that has to meet a couple of constraints. First, to serve the needs of international clients the cabin crew has to be able to speak German, Spanish, and French (see Table 5.2). Further, a minimal number of stewardesses resp. stewards have to attend a flight (see Table 5.3). Finally, every cabin crew member has two flights off after an attended flight.
|
|
Table 5.1: Cabin crew per flight.
|
Table 5.2: Cabin crew speaking foreign language per flight.
|
|
Table 5.3: Male resp. female cabin crew per flight.
Model
The cabin crew for every flight is represented as a set. The constraints on cabin crews of individual flights are modeled in terms of constraints on the cardinality of the intersection of the cabin crew set of that flight with the sets associated with particular restrictions. Therefore the following subsets of the cabin crew are introduced: male, female, Spanish-speaking, French-speaking, and German-speaking cabin crew. The constraint that a crew member has two flights off after an attended flight is expressed by the disjointness of the appropriate sets representing a crew per flight.
Solver
The function AssignCrew returns a solver configured according to its arguments FlightData and Crew. As previously mentioned, the constraints on the cabin crew of a flight are expressed in terms of sets of crew members meeting these constraints. For that reason the following variables are defined:
Stewards(male cabin crew members),Stewardesses(female cabin crew members),FrenchSpeaking,GermanSpeaking, andSpanishSpeaking(French-, German-, resp. Spanish-speaking cabin crew members).
Procedure TeamConstraint imposes the abovementioned constraints on the individual flight cabin crew sets intersecting them with appropriate sets (FS.intersection), and constrains the intersection's cardinality according to Table 5.1, Table 5.2, and Table 5.3 (using FS.card and >=:).
The procedure SequenceDisjoint is responsible to ensure that every crew member may enjoy a two-flight break between two flights. It is a recursive procedure imposing FS.disjoint upon every 3 subsequent sets.
The actual solver declares the local variable Flights that contains the list of sets representing the individual crew assignments. Then, the constraints of the procedure TeamConstraint are imposed on Flights by the Map loop, by mapping the data provided by FlightData to Flights. The distribution is straightforward and has no particularities.
Dealing with sets of literals
Often real-life applications deal with sets of names, descriptions and the like rather than integers, which can be represented by Oz literals. The functions SetOfLiterals, Lits2Ints, and Ints2Lits allow to model sets of literals. The function SetOfLiterals returns an abstract data structure that enables Lits2Ints and Ints2Lits to map literals to integers and vice versa. The last line of the solver procedure converts the internal solution to a representation corresponding to the format of AssignCrew's argument Crew (see below).
declare
local
Lit2Int = {NewName}
Int2Lit = {NewName}
in
fun {SetOfLiterals Lits}
sol(Lit2Int:
{NewChunk
{List.toRecord l2i
{List.mapInd Lits fun {$ I L}
L#I
end}}}
Int2Lit:
{NewChunk
{List.toRecord i2l
{List.mapInd Lits fun {$ I L}
I#L
end}}})
end
fun {Lits2Ints SetOfLiterals Literals}
{Map Literals fun {$ Lit}
SetOfLiterals.Lit2Int.Lit
end}
end
fun {Ints2Lits SetOfLiterals Ints}
{Map Ints fun {$ Int}
SetOfLiterals.Int2Lit.Int
end}
end
end
fun {CrewProb FlightData Crew}
CabinStaff = {Append Crew.stewards Crew.stewardesses}
CrewSet = {SetOfLiterals CabinStaff}
Stewards = {FS.value.make
{Lits2Ints CrewSet Crew.stewards}}
Stewardesses = {FS.value.make
{Lits2Ints CrewSet Crew.stewardesses}}
FrenchSpeaking = {FS.value.make
{Lits2Ints CrewSet Crew.frenchspeaking}}
GermanSpeaking = {FS.value.make
{Lits2Ints CrewSet Crew.germanspeaking}}
SpanishSpeaking = {FS.value.make
{Lits2Ints CrewSet Crew.spanishspeaking}}
proc {TeamConstraint Team Flight}
flight(no:_ crew:N stewards:NStew stewardesses:NHost
frenchspeaking:NFrench germanspeaking:NGerman
spanishspeaking:NSpanish) = Flight
in
{FS.card Team N}
{FS.card
{FS.intersect Team Stewards}} >=: NStew
{FS.card
{FS.intersect Team Stewardesses}} >=: NHost
{FS.card
{FS.intersect Team FrenchSpeaking}} >=: NFrench
{FS.card
{FS.intersect Team GermanSpeaking}} >=: NGerman
{FS.card
{FS.intersect Team SpanishSpeaking}} >=: NSpanish
end
proc {SequencedDisjoint L}
case L of A|B|C|T then
{FS.disjoint A B}
{FS.disjoint A C}
{SequencedDisjoint B|C|T}
elseof A|B|nil then
{FS.disjoint A B}
end
end
in
proc {$ Sol}
Flights = {FS.var.list.upperBound
{Length FlightData}
{Lits2Ints CrewSet CabinStaff}}
in
{Map FlightData proc {$ D F}
{TeamConstraint F D}
end Flights}
{SequencedDisjoint Flights}
{FS.distribute naive Flights}
Sol = {Map Flights
fun {$ F}
{Ints2Lits CrewSet {FS.monitorIn F}}
end}
end
end
The following sample data can be used to test the solver:
declare
Flights =
[flight(no: 1 crew:4 stewards:1 stewardesses:1
frenchspeaking:1 spanishspeaking:1
germanspeaking:1)
flight(no: 2 crew:5 stewards:1 stewardesses:1
frenchspeaking:1 spanishspeaking:1
germanspeaking:1)
flight(no: 3 crew:5 stewards:1 stewardesses:1
frenchspeaking:1 spanishspeaking:1
germanspeaking:1)
flight(no: 4 crew:6 stewards:2 stewardesses:2
frenchspeaking:1 spanishspeaking:1
germanspeaking:1)
flight(no: 5 crew:7 stewards:3 stewardesses:3
frenchspeaking:1 spanishspeaking:1
germanspeaking:1)
flight(no: 6 crew:4 stewards:1 stewardesses:1
frenchspeaking:1 spanishspeaking:1
germanspeaking:1)
flight(no: 7 crew:5 stewards:1 stewardesses:1
frenchspeaking:1 spanishspeaking:1
germanspeaking:1)
flight(no: 8 crew:6 stewards:1 stewardesses:1
frenchspeaking:1 spanishspeaking:1
germanspeaking:1)
flight(no: 9 crew:6 stewards:2 stewardesses:2
frenchspeaking:1 spanishspeaking:1
germanspeaking:1)
flight(no:10 crew:7 stewards:3 stewardesses:3
frenchspeaking:1 spanishspeaking:1
germanspeaking:1)]
Crew =
crew(stewards:
[tom david jeremy ron joe bill fred bob mario ed]
stewardesses:
[carol janet tracy marilyn carolyn cathy inez
jean heather juliet]
frenchspeaking:
[inez bill jean juliet]
germanspeaking:
[tom jeremy mario cathy juliet]
spanishspeaking:
[bill fred joe mario marilyn inez heather])
Running the solver by {ExploreOne {AssignCrew Flights Crew}}. and invoking the Oz Browser on the solution node results in:
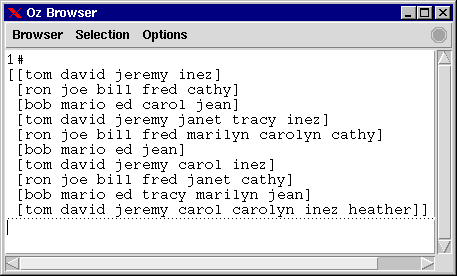
The flights are to be attended in the order they appear in the solution list. Each sublist denotes the assignment for an individual flight.